- ГАТО ГРАДИЕНТ
функционала
 в точке
в точке  гильбертова пространства H - вектор из H, равный Гато производной
гильбертова пространства H - вектор из H, равный Гато производной функционала f в точке
функционала f в точке  . Иначе говоря, Г. г. определяется формулой
. Иначе говоря, Г. г. определяется формулой

где
 при
при  . В га-мерном евклидовом пространстве Г. г.
. В га-мерном евклидовом пространстве Г. г.  есть вектор с координатами
есть вектор с координатами

и наз. обычно градиентом. Понятие Г. г. распространяется на случай, когда X- риманово многообразие (конечномерное или гильбертово бесконечномерное), а
 - гладкая действительная функция на X. Направление вдоль Г. г. среди всех направлений, проходящих через точку
- гладкая действительная функция на X. Направление вдоль Г. г. среди всех направлений, проходящих через точку 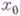 , выделяется наибольшим ростом функции
, выделяется наибольшим ростом функции  .
. В. М .Тихомиров.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
