ГАРМОНИЧЕСКОЙ МЕРЫ ПРИНЦИП

при отображениях, осуществляемых однозначными аналитич. функциями, гармоническая мера не убывает. Если

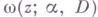- гармонич. мера граничного множества 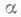относительно области Dна плоскости комплексного переменного z, то одна из конкретных формулировок Г. м. п. утверждает следующее. Пусть в области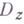

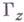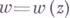с границей , состоящей из конечного числа жордановых дуг, задана однозначная аналитич. функция , удовлетворяющая условиям: значения , попадают в область с границей состоящей из конечного числа жордановых дуг; функция непрерывно продолжается на нек-рое множество состоящее из конечного числа дуг, и значения на принадлежат множеству с границей , состоящей из конечного числа жордановых дуг. При этих условиях во всякой точке zО D_z в к-рой имеет место соотношение

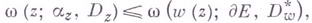(1)

где обозначает подобласть 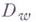такую, что точка Если в (1) имеет место равенство в какой-либо одной точке z, то оно будет иметь место всюду в . В частности, при взаимно однозначном конформном отображении на выполняется тождество

Г. м. п. был установлен Р. Неванлипной, давшим ему Многочисленные применения (см. [1], [2]). Например, из Г. м. п. выводится двух констант теорема, из к-рой, в свою очередь, следует, что для функции , голоморфной в области , максимальное значение функции на линии уровня является выпуклой функцией параметра .

Г. м. п. обобщается для голоморфных функций нескольких комплексных переменных,.

Лит.:[1] Nevanlinna F., Nevanlinna R., "Acta Soc. sclent, fennica", 1922, n. 50, № 5, p. 1-46; [2] Неванлинна Р., Однозначные аналитические функции, пер. с нем., М.-Л., 1941. П. М. Тамразое.