Волновое уравнение

        дифференциальное уравнение с частными производными, описывающее процесс распространения возмущений в некоторой среде. В случае малых возмущений и однородной изотропной среды В. у. имеет вид:

        

        где х, у, z — пространственные переменные, t — время, u = u (х, у, z) — искомая функция, характеризующая возмущение в точке (х, у, z) в момент t, а — скорость распространения возмущения. В. у. является одним из основных уравнений математической физики и широко используется в приложениях. Если u зависит только от двух (одной) пространственных переменных, то В. у. упрощается и называется двумерным (одномерным). В. у. допускает решение в виде «расходящейся сферической волны»:

         u = f (t - r/a)/r,

        где f — произвольная функция, a

        

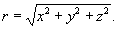         Особый интерес представляет так называемое элементарное решение (элементарная волна):

         u = δ (t - r/a)/r

        (где δ — Дельта-функция), дающее процесс распространения возмущения, произведённого мгновенным точечным источником (действовавшим в начале координат при t = 0). Образно говоря, элементарная волна представляет собой «бесконечный всплеск» на окружности r = at, удаляющийся от начала координат со скоростью а с постепенным уменьшением интенсивности. При помощи наложения элементарных волн можно описать процесс распространения произвольного возмущения.

         Малые колебания струны описываются одномерным В. у.:

        

        Ж. Д'Аламбер предложил (1747) метод решения этого В. у. в виде наложения прямой и обратной волн: u = f (x - at) + g (x + at), а Л. Эйлер (1748) установил, что функции f и g определяются заданием так называемых начальных условий (См. Начальное условие).

         Лит.: Тихонов А. Н. и Самарский А. А., Уравнения математической физики, 3 изд., М., 1966.

         П. И. Лизоркин.