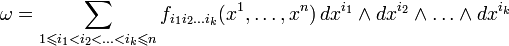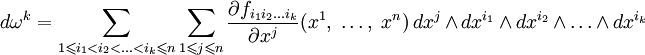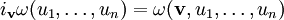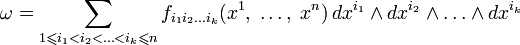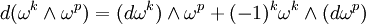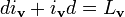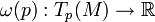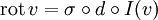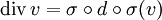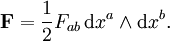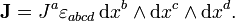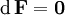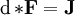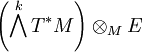Внешний дифференциал

Дифференциа́льная фо́рма порядка k или k-форма — кососимметрическое тензорное поле типа 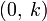$(0,\;k)$ на касательном расслоении многообразия.

Дифференциальные формы были введены Картаном в начале XX века.

Формализм дифференциальных форм оказывается удобен во многих разделах теоретической физики и математики, в частности, в теоретической механике, симплектической геометрии, квантовой теории поля.

Пространство k-форм на многообразии M обычно обозначают Ω^k(M).

Определения

Инвариантное

В дифференциальной геометрии, дифференциальная форма степени k — это гладкое сечение k-ой внешней степени кокасательного расслоения многообразия.

Через локальные карты

k-формой на $\mathbb{R}^n$ будем называть выражение следующего вида

$\omega=\sum_{1\leqslant i_1<i_2<\ldots<i_k\leqslant n}f_{i_1i_2\ldots i_k}(x^1,\ldots,x^n)\,dx^{i_1}\wedge dx^{i_2}\wedge\ldots\wedge dx^{i_k}$

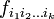где $f_{i_1i_2\ldots i_k}$ — гладкие функции, dxⁱ — дифференциал i-ой координаты xⁱ (функция от вектора, возвращающая его координату с номером i ), а 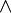$\wedge$ — внешнее произведение. При смене координат, это представление меняет форму.

На гладком многообразии, k-формы могут быть определены как формы на картах, которые согласованы на склейках (для точного определения согласованности см. многообразие).

Связанные определения

• Для k-формы ω^k, её внешний дифференциал это (k + 1)-форма

• $d\omega^k=\sum_{1\leqslant i_1<i_2<\ldots<i_k\leqslant n}\sum_{1\leqslant j\leqslant n}\frac{\partial f_{i_1i_2\ldots i_k}}{\partial x^j}(x^1,\;\dots,\;x^n)\,dx^j\wedge dx^{i_1}\wedge dx^{i_2}\wedge\ldots\wedge dx^{i_k}$

• Дифференциальная форма называется замкнутой, если её внешняя производная равна 0.
• k-форма называется точной, если её можно представить как дифференциал некоторой (k-1)-формы.
• Факторгруппа 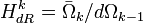$H^k_{dR} = \bar\Omega_{k} / d\Omega_{k-1}$ замкнутых k-форм по точным k-формам называется k-мерной группой когомологий де Рама. Теорема де Рама утверждает, что она изоморфна k-мерной группе сингулярных когомологий.
• Внутренней производной формы ω по векторному полю 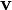$\mathbf{v}$ называется форма

$i_\mathbf{v} \omega (u_1, \dots, u_n) = \omega(\mathbf{v}, u_1, \dots, u_n)$

Свойства

• В локальных координатах, дифференциальная форма может быть записана как

  $\omega=\sum_{1\leqslant i_1<i_2<\ldots<i_k\leqslant n}f_{i_1i_2\ldots i_k}(x^1,\;\ldots,\;x^n)\,dx^{i_1}\wedge dx^{i_2}\wedge\ldots\wedge dx^{i_k}$

где dxⁱ — дифференциал i-ой координаты x^j, а 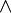$\wedge$ — внешнее произведение.

• Дифференциальную форму можно рассматривать как поле полилинейных кососимметрических функций от k векторов.
• Внешнее дифференцирование линейно и удовлетворяет градуированному правилу Лейбница:

  $\ d (\omega^k \wedge\omega^p) = (d\omega^k) \wedge\omega^p + (-1)^{k}\omega^k \wedge(d \omega^p)$

• Для любой формы справедливо d(dω) = 0.
• теорема Стокса — является основой для большинства применений дифференциальных форм.
• Внутреннее дифференцирование линейно и удовлетворяет градуированному правилу Лейбница. Оно связано с внешним дифференцированием и производной Ли формулой гомотопии:

  $d i_\mathbf{v} + i_\mathbf{v} d = L_\mathbf{v}$

Примеры

• С точки зрения тензорного анализа, 1-форма есть не что иное как ковекторное поле, то есть 1 раз ковариантный тензор, заданный в каждой точке p многообразия M и отображающий элементы касательного пространства T_p(M) в множество вещественных чисел $\R$:

  $\omega(p): T_p (M)\rightarrow \R$

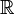• Форма объёма — пример n-формы на n-мерном многообразии.
• Симплектическая форма — замкнутая 2-форма ω на 2n-многообразии, такая что $\omega^n\not=0$.

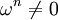Применения

Векторный анализ

Основная статья: Векторный анализ

Через дифференциальные формы возможно представить основные операторы в векторном анализе Пусть I — канонический изоморфизм между касательным и кокасательным пространствами, и σ — канонический изоморфизм между 2-формами и векторными полями на M. Благодаря этому можно определить дифференциальные операции с векторными полями на M. Тогда ротор и дивергенцию для полей на 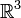$\R^3$ можно представить как

$\operatorname{rot}\,v = \sigma\circ d\circ I (v)$

$\operatorname{div}\,v = \sigma\circ d\circ \sigma (v)$

Дифференциальные формы в электродинамике

Основная статья: Калибровочная инвариантность

Максвелловская электродинамика весьма изящно формулируется на языке дифференциальных форм. Рассмотрим 2-форму Фарадея, соответствующую тензору электромагнитного поля:

$\textbf{F} = \frac{1}{2}F_{ab}\, {\mathrm d}x^a \wedge {\mathrm d}x^b.$

Эта форма является формой кривизны тривиального главного расслоения со структурной группой U(1), с помощью которого могут быть описаны классическая электродинамика и калибровочная теория. 3-форма тока имеет вид

$\textbf{J} = J^a \varepsilon_{abcd}\, {\mathrm d}x^b \wedge {\mathrm d}x^c \wedge {\mathrm d}x^d.$

В этих обозначениях уравнения Максвелла могут быть очень компактно записаны как

$\mathrm{d}\, {\textbf{F}} = \textbf{0}$

$\mathrm{d}\, {*\textbf{F}} = \textbf{J}$

где * — оператор звезды Ходжа. Подобным образом может быть описана геометрия общей калибровочной теории.

2-форма 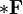$* \mathbf{F}$ также называется 2-формой Максвелла.

Гамильтонова механика

Основная статья: Гамильтонова механика

С помощью дифференциальных форм можно сформулировать гамильтонову механику чисто геометрически. Рассмотрим симплектическое многообразие M с заданными на нём симплектической формой ω и функцией H, называемой функцией Гамильтона. ω задаёт в каждой точке 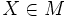$X \in M$ изоморфизм I касательного T_XM и кокасательного 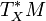$T^{*}_{X}M$ пространств по правилу

$dH( \mathbf{u} ) = \omega ( I dH, \mathbf{u}), ~~ \forall\mathbf{u} \in T_{X}M$,

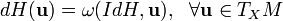где dH — 1-форма дифференциала функции H. Векторное поле IdH на многообразии называется гамильтоновым полем, а соответствующий ему фазовый поток — гамильтоновым потоком. Гамильтонов фазовый поток сохраняет симплектическую форму, а следовательно, сохраняет и любую её внешнюю степень. Отсюда следует теорема Лиувилля. Скобка Пуассона функций F и G на M определяется по правилу

[F,G] = ω(IdF,IdG)

Вариации и обобщения

Помимо вещественно- и комплекснозначных форм, часто также рассматриваются дифференциальные формы со значениями в векторных расслоениях. В этом случае в каждой точке задается полилинейная антисимметричная функция от k векторов из касательного расслоения, возвращающая вектор из слоя над этой точкой. Формально внешние k-формы на M со значениями в векторном расслоении 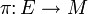$\pi\colon E \to M$ определяются как сечения тензорного произведения расслоений

$\left(\bigwedge^k T^*M\right) \otimes_{M} E$

Частный случай векторнозначных дифференциальных форм — тангенциальнозначные формы, в определении которых в качестве векторного расслоения берётся касательное расслоение TM.

Литература

• Арнольд В. И. Математические методы классической механики. — 5-е изд., стереотипное. — М.: Едиториал УРСС, 2003. — 416 с. — 1500 экз. — ISBN 5-354-00341-5
• Годбийон К. Дифференциальная геометрия и аналитическая механика. — М.: Мир, 1971.
• Дубровин Б.А., Новиков С.П., Фоменко А.Т. Современная геометрия. Методы и приложения. — М.: Наука, 1971.
• Картан А. Дифференциальное исчисление. Дифференциальные формы. — М.: Мир, 1971.
• Постников М.М. Лекции по геометрии. Семестр III. Гладкие многообразия. — М.: Наука, 1987.

См. также

• Внешняя алгебра
• Когомологии де Рама
• Теорема Стокса
• Дифференциальные формы в электродинамике