ВЕРОЯТНОСТНОЕ ПРОСТРАНСТВО
- ВЕРОЯТНОСТНОЕ ПРОСТРАНСТВО
поле вероятностей,- совокупность  непустого множества
непустого множества  , класса
, класса  подмножеств множества Q, являющегося борелевским полем (т. е. замкнутым относительно теоретико-множественных операций, производимых в счетном числе) и распределения ( вероятностной мери)
подмножеств множества Q, являющегося борелевским полем (т. е. замкнутым относительно теоретико-множественных операций, производимых в счетном числе) и распределения ( вероятностной мери)  на
на  . Понятие В. п. принадлежит А. Н. Колмогорову [1]. Точки множества
. Понятие В. п. принадлежит А. Н. Колмогорову [1]. Точки множества  наз. элементарными событиями, а само множество
наз. элементарными событиями, а само множество  - пространством элементарных событий. Принадлежащие
- пространством элементарных событий. Принадлежащие  подмножества множества
подмножества множества  наз. (случайными) событиями. Нередко ограничиваются рассмотрением лишь полных В. п., то есть пространств, удовлетворяющих требованию
наз. (случайными) событиями. Нередко ограничиваются рассмотрением лишь полных В. п., то есть пространств, удовлетворяющих требованию  . Если
. Если  - произвольное В. п., то класс множеств вида
- произвольное В. п., то класс множеств вида  , где
, где  и
и  образует борелевское поле
образует борелевское поле 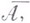 а функция
а функция  на
на  определяемая формулой
определяемая формулой  есть распределение на
есть распределение на  Пространство
Пространство  полно и наз. пополнением
полно и наз. пополнением  . Иногда также ограничиваются рассмотрением лишь совершенны х В. п., то есть таких, что для любой действительной
. Иногда также ограничиваются рассмотрением лишь совершенны х В. п., то есть таких, что для любой действительной  -измеримой функции f и любого множества Ена прямой, для к-рого
-измеримой функции f и любого множества Ена прямой, для к-рого  существует борелевское множество Втакое, что
существует борелевское множество Втакое, что  и
и 
 . В рамках совершенных В. п. невозможны нек-рые "патологические" явления (связанные с существованием условных вероятностей, определением независимых случайных величин и т. д.), возникающие в общей схеме. Не всегда тривиален вопрос о существовании В. п., удовлетворяющего тем или иным специальным требованиям. Одним из результатов такого рода является фундаментальная теорема Колмогорова о согласованных распределениях: пусть каждому упорядоченному конечному набору
. В рамках совершенных В. п. невозможны нек-рые "патологические" явления (связанные с существованием условных вероятностей, определением независимых случайных величин и т. д.), возникающие в общей схеме. Не всегда тривиален вопрос о существовании В. п., удовлетворяющего тем или иным специальным требованиям. Одним из результатов такого рода является фундаментальная теорема Колмогорова о согласованных распределениях: пусть каждому упорядоченному конечному набору  элементов множества Тотвечает распределение
элементов множества Тотвечает распределение  на борелевских множествах евклидова пространства
на борелевских множествах евклидова пространства 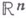 и пусть выполнены следующие условия согласованности:
и пусть выполнены следующие условия согласованности:

Тогда на наименьшем борелевском поле  подмножеств произведения
подмножеств произведения  относительно к-рого'измеримы все координатные функции
относительно к-рого'измеримы все координатные функции  существует распределение
существует распределение 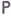 такое, что для любого конечного подмножества
такое, что для любого конечного подмножества  множества Ти любого и-мерного борелевского множества Всправедливо равенство:
множества Ти любого и-мерного борелевского множества Всправедливо равенство:

Лит.:[l] Колмогоров А. Н., Основные понятия теории вероятностей, 2 изд., М., 1974; [2] Гнеденко Б. В., Колмогоров А. Н., Предельные распределения для сумм независимых случайных величин, М.-Л., 1949; [3] Неве Ж., Математические основы теории вероятностей, пер. с франц., М., 1969. В. В. Сазонов.
Математическая энциклопедия. — М.: Советская энциклопедия.
И. М. Виноградов.
1977—1985.
Полезное
Смотреть что такое "ВЕРОЯТНОСТНОЕ ПРОСТРАНСТВО" в других словарях:
Вероятностное пространство — У этого термина существуют и другие значения, см. Пространство. Вероятностное пространство понятие, введённое А. Н. Колмогоровым в 30 х годах XX века для формализации понятия вероятности, которое дало начало бурному развитию теории вероятностей… … Википедия
Пространство (физика) — Пространство понятие, используемое (непосредственно или в составе сложных терминов) в естественных языках, а также в таких разделах знания, как философия, математика, физика и т. п. На уровне повседневного восприятия пространство интуитивно… … Википедия
Пространство (значения) — Пространство понятие, используемое (непосредственно или в словосочетаниях) в обыденной речи, а также в различных разделах знаний. Пространство на уровне повседневного восприятия Математика Трёхмерное пространство Аффинное пространство Банахово… … Википедия
Пространство (математика) — У этого термина существуют и другие значения, см. Пространство. В математике слово «пространство» употребляется в большом наборе сложных терминов. Грубо говоря, пространство есть множество с некоторой дополнительной структурой. В зависимости от… … Википедия
Пространство элементарных событий — Пространство элементарных событий множество всех различных исходов случайного эксперимента. Элемент этого множества называется элементарным событием или исходом. Пространство элементарных событий называется дискретным, если число его… … Википедия
РАСПРЕДЕЛЕНИЕ ВЕРОЯТНОСТЕЙ (ВЕРОЯТНОСТНОЕ РАСПРЕДЕЛЕНИЕ) — одно из основных понятий теории вероятностей (см.) и статистики математической (см.). При современном подходе в качестве математич. модели изучаемого случайного явления берется соответствующее вероятностное пространство { F 1, S, Р), где Q… … Российская социологическая энциклопедия
ВЫБОРОЧНОЕ ПРОСТРАНСТВО — множество всех элементарных событии, связанных с нек рым экспериментом, причем любой неразложимый исход эксперимента представляется одной и только одной точкой В. п. (выборочной точкой). В. п. является абстрактным множеством, на алгебре… … Математическая энциклопедия
Неравенство Гёльдера — в функциональном анализе и смежных дисциплинах это фундаментальное свойство пространств . Содержание 1 Формулировка 2 Доказательство … Википедия
Неравенство Минковского — это неравенство треугольника для пространств функций с интегрируемой ой степенью. Содержание 1 Формулировка 2 Доказательство … Википедия
Гёльдера неравенство — Неравенство Гёльдера в функциональном анализе и смежных дисциплинах это фундаментальное свойство пространств Lp. Содержание 1 Формулировка 2 Частные случаи 2.1 Неравен … Википедия
 непустого множества
непустого множества  , класса
, класса  подмножеств множества Q, являющегося борелевским полем (т. е. замкнутым относительно теоретико-множественных операций, производимых в счетном числе) и распределения ( вероятностной мери)
подмножеств множества Q, являющегося борелевским полем (т. е. замкнутым относительно теоретико-множественных операций, производимых в счетном числе) и распределения ( вероятностной мери)  на
на  . Понятие В. п. принадлежит А. Н. Колмогорову [1]. Точки множества
. Понятие В. п. принадлежит А. Н. Колмогорову [1]. Точки множества  наз. элементарными событиями, а само множество
наз. элементарными событиями, а само множество  - пространством элементарных событий. Принадлежащие
- пространством элементарных событий. Принадлежащие  подмножества множества
подмножества множества  наз. (случайными) событиями. Нередко ограничиваются рассмотрением лишь полных В. п., то есть пространств, удовлетворяющих требованию
наз. (случайными) событиями. Нередко ограничиваются рассмотрением лишь полных В. п., то есть пространств, удовлетворяющих требованию  . Если
. Если  - произвольное В. п., то класс множеств вида
- произвольное В. п., то класс множеств вида  , где
, где  и
и  образует борелевское поле
образует борелевское поле 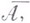 а функция
а функция  на
на  определяемая формулой
определяемая формулой  есть распределение на
есть распределение на  Пространство
Пространство  полно и наз. пополнением
полно и наз. пополнением  . Иногда также ограничиваются рассмотрением лишь совершенны х В. п., то есть таких, что для любой действительной
. Иногда также ограничиваются рассмотрением лишь совершенны х В. п., то есть таких, что для любой действительной  -измеримой функции f и любого множества Ена прямой, для к-рого
-измеримой функции f и любого множества Ена прямой, для к-рого  существует борелевское множество Втакое, что
существует борелевское множество Втакое, что  и
и 
 . В рамках совершенных В. п. невозможны нек-рые "патологические" явления (связанные с существованием условных вероятностей, определением независимых случайных величин и т. д.), возникающие в общей схеме. Не всегда тривиален вопрос о существовании В. п., удовлетворяющего тем или иным специальным требованиям. Одним из результатов такого рода является фундаментальная теорема Колмогорова о согласованных распределениях: пусть каждому упорядоченному конечному набору
. В рамках совершенных В. п. невозможны нек-рые "патологические" явления (связанные с существованием условных вероятностей, определением независимых случайных величин и т. д.), возникающие в общей схеме. Не всегда тривиален вопрос о существовании В. п., удовлетворяющего тем или иным специальным требованиям. Одним из результатов такого рода является фундаментальная теорема Колмогорова о согласованных распределениях: пусть каждому упорядоченному конечному набору  элементов множества Тотвечает распределение
элементов множества Тотвечает распределение  на борелевских множествах евклидова пространства
на борелевских множествах евклидова пространства 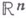 и пусть выполнены следующие условия согласованности:
и пусть выполнены следующие условия согласованности:
 подмножеств произведения
подмножеств произведения  относительно к-рого'измеримы все координатные функции
относительно к-рого'измеримы все координатные функции  существует распределение
существует распределение 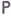 такое, что для любого конечного подмножества
такое, что для любого конечного подмножества  множества Ти любого и-мерного борелевского множества Всправедливо равенство:
множества Ти любого и-мерного борелевского множества Всправедливо равенство:
