- БЕРНУЛЛИ ИСПЫТАНИЯ
независимые испытания с двумя исходами каждое ("успехом" и "неудачей") и такие, что вероятности исходов не изменяются от испытания к испытанию. Б. и. служат одной из основных схем, рассматриваемых в теории вероятностей.
Пусть р - вероятность успеха и
 - вероятность неудачи, и пусть 1 обозначает наступление успеха, а 0 - наступление неудачи. Тогда вероятность определенного чередования успехов и неудач, напр.,
- вероятность неудачи, и пусть 1 обозначает наступление успеха, а 0 - наступление неудачи. Тогда вероятность определенного чередования успехов и неудач, напр.,

равна

где
 - число успехов в рассматриваемом ряду писпытаний. Со схемой Б. и. связаны многие распространенные распределения вероятностей. Пусть
- число успехов в рассматриваемом ряду писпытаний. Со схемой Б. и. связаны многие распространенные распределения вероятностей. Пусть  - случайная величина, равная числу успехов в пБ. и. Тогда вероятность события
- случайная величина, равная числу успехов в пБ. и. Тогда вероятность события  равна
равна

т. е.
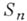 имеет биномиальное распределение. Последнее при
имеет биномиальное распределение. Последнее при  аппроксимируется нормальным распределением или Пуассона распределением. Пусть
аппроксимируется нормальным распределением или Пуассона распределением. Пусть  - число испытаний до первого успеха. Тогда вероятность события
- число испытаний до первого успеха. Тогда вероятность события  равна
равна  т. е.
т. е.  имеет геометрическое распределение. Если
имеет геометрическое распределение. Если  - число неудач, предшествующих r-му появлению успеха, то
- число неудач, предшествующих r-му появлению успеха, то  имеет так наз. отрицательное биномиальное распределение. Число успехов
имеет так наз. отрицательное биномиальное распределение. Число успехов  в Б. и. можно представить в виде суммы
в Б. и. можно представить в виде суммы  независимых случайных величин, где
независимых случайных величин, где 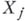 равно 1, если
равно 1, если  испытание закончилось успехом, и равно 0 в противном случае. Поэтому многие важные закономерности теории вероятностей, относящиеся к суммам независимых случайных величин, были первоначально установлены для схемы Б. и. ( Бернулли теорема, больших чисел закон, больших чисел усиленный закон, повторного логарифма закон, Центральная предельная теорема и т. д. ). Строгое изучение бесконечных последовательностей Б. и. требует введения вероятностной меры, в пространстве бесконечных последовательностей нулей и единиц. Это можно сделать или непосредственно, или с помощью приема, к-рый иллюстрируется ниже случаем
испытание закончилось успехом, и равно 0 в противном случае. Поэтому многие важные закономерности теории вероятностей, относящиеся к суммам независимых случайных величин, были первоначально установлены для схемы Б. и. ( Бернулли теорема, больших чисел закон, больших чисел усиленный закон, повторного логарифма закон, Центральная предельная теорема и т. д. ). Строгое изучение бесконечных последовательностей Б. и. требует введения вероятностной меры, в пространстве бесконечных последовательностей нулей и единиц. Это можно сделать или непосредственно, или с помощью приема, к-рый иллюстрируется ниже случаем  . Пусть
. Пусть  - число, выбираемое наудачу на отрезке
- число, выбираемое наудачу на отрезке  с равномерным распределением, и пусть
с равномерным распределением, и пусть
где
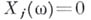 или 1, есть разложение со в двоичную дробь. Тогда
или 1, есть разложение со в двоичную дробь. Тогда  независимы и принимают значения 0 и 1 с вероятностью
независимы и принимают значения 0 и 1 с вероятностью  каждое, т. е. чередование нулей и единиц в двоичном разложении w описывается схемой Б. и. с
каждое, т. е. чередование нулей и единиц в двоичном разложении w описывается схемой Б. и. с  Однако меру на (0, 1) можно задать и так, чтобы получить Б. и. с любым р (при
Однако меру на (0, 1) можно задать и так, чтобы получить Б. и. с любым р (при  получается мера, сингулярная относительно меры Лебега).
получается мера, сингулярная относительно меры Лебега).
Б. и. часто трактуют геометрически (см. Бернулли блуждание). Ряд вероятностей, связанных с Б. и., был вычислен на самой ранней ступени развития теории вероятностей в связи с задачей о разорении игроков.
Лит.:[1] Гнеденко Б. В., Курс теории вероятностей, 5 изд., М., 1969; [2] Феллер В., Введение в теорию вероятностей и ее приложения, пер. с англ., 2 изд., т. 1-2, М., 1967; [3] Кац М., Статистическая независимость в теории вероятностей, анализе и теории чисел, пер. с англ., М., 1963.
А. В. Прохоров.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
