ОБРАТИМЫЙ ПУЧОК

ОБРАТИМЫЙ ПУЧОК

- локально свободный пучок -модулей ранга 1 на окольцованном пространстве '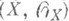. Эквивалентное определение О. п.: пучок -модулей, локально изоморфный пучку . О. п. на X, рассматриваемые с точностью до изоморфизма, образуют абелеву группу относительно операции тензорного умножения над . Эта группа наз. Пикара группой пространства Xи обозначается Pic X. Обратным к пучку.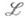 будет в ней пучок двойственный к . В случае, когда - схема (в частности, алгебраич. многообразие) или аналитич. ространство, пучок -модулей обратим тогда и только тогда, когда он изоморфен пучку регулярных (соответственно аналитических) сечений нек-рого линейного алгебраического (соответственно аналитического) расслоения над X.

О. п. на схемах тесно связаны с дивизорами. Каждому дивизору Картье Dна Xсопоставляется О. п. чем определяется инъективный гомоморфизм , где - группа классов дивизоров Картье на X. Для целых схем Xэтот гомоморфизм является изоморфизмом.

На проективной схеме Xопределяется подкручивающий обратимый пучок Серра . А именно, если задано вложение схемы X в проективное пространство , то соответствует классу гиперплоского сечения. В частности, если - проективное пространство над полем к, то пучок есть прямой образ пучка линейных функций на при естественном отображении ... Систему однородных координат в можно отождествить с базисом пространства сечений

О. п. на схеме Xнад полем ксвязаны с рациональными отображениями схемы Xв проективные пространства. Пусть ' - О. п. на схеме - сечения пучка , значения к-рых в любой точке порождают слой над . Тогда существует единственный морфнзм такой, что и где - однородные координаты в . О. п.на Xназ. очень обильным, если существует такое вложение что . О. п.на Xназ. обильным, если существует такое целое положительное п, что очень обилен. На нётеровой схеме Xнад кобратимый пучок обилен тогда и только тогда, когда для каждого когерентного пучка , на Xсуществует такое целое n о>0, что пучок порождается при , своими глобальными сечениями.

Если - обильный О. п. на X, соответствующий дивизору D, то Dназ. обильным дивизором. Дивизор Картье Dна схеме X, собственной над алгебраически замкнутым полем к, обилен тогда и только тогда, когда для каждой замкнутой целой подсхемы индекс пересечения положителен, где r= dim Y. По поводу других критериев обильности см. [5]. Существует также обобщение понятия обильного дивизора на подмногообразия большей коразмерности [2].

Понятия очень обильного и обильного О. п. переносятся также на случай аналитич. ространств (по поводу критериев обильности в этой ситуации см. Положительное расслоение).

Лит.:[1] Hartshorne R., Algebraic geometry, N. Y., 1977; [2] его же, Ample subvarieties of algebraic varieties, N. Y. - В., 1970; [3] Мамфорд Д., Лекции о кривых на алгебраической поверхности, пер. с англ., М., 1968; [4] Шафаревич И. Р., Основы алгебраической геометрии, М., 1972; [5] Итоги науки и техники. Алгебра. Топология. Геометрия, т. 10, М., 1972, с. 47 -112.

В. А. Псковских.


Математическая энциклопедия. — М.: Советская энциклопедия. . 1977—1985.

Игры ⚽ Поможем сделать НИР

Полезное


Смотреть что такое "ОБРАТИМЫЙ ПУЧОК" в других словарях:

  • НОРМАЛЬНЫЙ ПУЧОК — аналог нормального расслоения в теории пучков. Пусть морфизм окольцованных пространств такой, что гомоморфизм сюръективен, и пусть Тогда есть пучок идеалов в и поэтому является модулем. Пучок …   Математическая энциклопедия

  • ОБИЛЬНЫЙ ПУЧОК — обобщение понятия обильного обратимого пучка. Пусть X нётерова схема над полем локально свободный пучок на X(т. е. пучок сечений нек рого векторного алгебраич. расслоения ). Пучок наз. обильным, если для всякого когерентного пучка на существует… …   Математическая энциклопедия

  • ЛИНЕЙЧАТАЯ ПОВЕРХНОСТЬ — в дифференциальной геометрии поверхность, образованная движением прямой линии. Прямые, принадлежащие этой поверхности, называются прямолинейными образующими, а каждая кривая, пересекающая все прямолинейные образующие, направляющей кривой. Если… …   Математическая энциклопедия

  • ДВОЙСТВЕННОСТЬ — 1) Д. в алгебраической геометрии двойственность между различными пространствами когомологий на алгебраич. многообразиях. Когомологий когерентных пучков. Пусть X неособое проективное алгебраич. многообразие размерности nнад алгебраически замкнутым …   Математическая энциклопедия

  • ДИВИЗОР — обобщение понятия делителя элемента коммутативного кольца. Впервые (под назв. идеальный делитель ) это понятие возникло в работах Э. Куммера [1] об арифметике круговых полей. Теория Д. для коммутативного кольца А с единицей без делителей нуля… …   Математическая энциклопедия

  • ПРОЕКТИВНЫЙ СПЕКТР — кольца схема Х = = Proj(R), сопоставляемая градуированному кольцу . Как множество точек X представляет собою множество однородных простых идеалов , таких, что . Топология на Xопределяется следующим базисом открытых множеств: для , п>0.… …   Математическая энциклопедия

  • ГИЛЬБЕРТА МНОГОЧЛЕН — градуированного модуля многочлен, выражающий при больших натуральных празмерности однородных слагаемых модуля как функцию от п. Более точно, справедлива теорема, доказанная по существу Д. Гильбертом. Пусть кольцо многочленов над полем К,… …   Математическая энциклопедия

  • ЛИНЕЙНАЯ СИСТЕМА — семейство эффективных линейно эквивалентных дивизоров на алгебраич. многообразии, параметризованное проективным пространством. Пусть X неособое алгебраич. многообразие над полем k, обратимый пучок на X, Г (X, ) пространство глобальных сечений… …   Математическая энциклопедия

  • ПРОЕКТИВНАЯ СХЕМА — замкнутая подсхема проективного пространства ; в однородных координатах x0, . . ., х п на проективная схема задается системой однородных алгебраич. уравнений: Каждая П. с. является полной (компактной в случае k= ); обратно, полная схема… …   Математическая энциклопедия

  • ХИМИЯ КОЛЛОИДНАЯ — раздел физической химии, занимающийся изучением коллоидных дисперсных систем (дисперсий), в которых одно мелкораздробленное вещество дисперсная фаза равномерно распределено (диспергировано) в другой фазе дисперсионной среде. В коллоидных системах …   Энциклопедия Кольера


Поделиться ссылкой на выделенное

Прямая ссылка:
… Нажмите правой клавишей мыши и выберите «Копировать ссылку»