- ДИОФАНТОВО МНОЖЕСТВО
- множество
 состоящее из упорядоченных наборов из пцелых (целых неотрицательных, целых положительных) чисел, для к-рого можно указать диофантово уравнение
состоящее из упорядоченных наборов из пцелых (целых неотрицательных, целых положительных) чисел, для к-рого можно указать диофантово уравнение
зависящее от ппараметров а 1, ..., а п, допустимыми значениями к-рых являются целые (соответственно целые неотрицательные или целые положительные), числа, и разрешимое относительно х 1, ..., xl тогда и только тогда, когда
 Здесь несущественно, понимается ли под разрешимостью существование решения в целых, целых неотрицательных или целых положительных числах, поскольку уравнение (*) разрешимо в целых (целых неотрицательных, целых положительных) числах тогда и только тогда, когда уравнение
Здесь несущественно, понимается ли под разрешимостью существование решения в целых, целых неотрицательных или целых положительных числах, поскольку уравнение (*) разрешимо в целых (целых неотрицательных, целых положительных) числах тогда и только тогда, когда уравнение
разрешимо в целых положительных числах (соответственно тогда и только тогда, когда уравнение

разрешимо в целых неотрицательных числах, или соответственно тогда и только тогда, когда уравнение

разрешимо в целых числах, ибо по теореме Лагранжа каждое целое неотрицательное число представимо в виде суммы четырех квадратов).
Для любого Д. м. можно указать соответствующее уравнение (*), в к-ром степень многочлена Рне больше 4 (это достигается ценой увеличения числа неизвестных). Для каждого Д. м. целых неотрицательных чисел, помимо уравнения общего вида (*), можно указать уравнение вида Р( х 1,..., xl) = а 1; иными словами, каждое Д. м. целых неотрицательных чисел является множеством всех неотрицательных значений, принимаемых некоторым многочленом с целочисленными коэффициентами при произвольных значениях переменных. В качестве Рвсегда можно взять многочлен степени не выше 5, если допустимыми значениями переменных являются целые неотрицательные или целые положительные числа, и многочлен степени не выше 6, если переменные принимают произвольные целочисленные значения.
Класс Д. м. замкнут относительно операций перестановки и отождествления аргументов, объединения, пересечения, прямого произведения и проектирования (проекцией множества
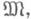 состоящего из упорядоченных наборов из п чисел, наз. множество
состоящего из упорядоченных наборов из п чисел, наз. множество а также относительно операции, ставящей множеству
а также относительно операции, ставящей множеству 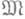 в соответствие множество
в соответствие множество
Класс Д. м. совпадает с классом перечислимых множеств (см. Диофантовых уравнений проблема разрешимости), и все результаты о перечислимых множествах переносятся на Д. м. В частности, из теоремы о существовании универсального перечислимого множества следует, что существует такое число l, что для каждого псуществует многочлен Un(a1, . . ., а п, т, х 1, . .., х l )с целочисленными коэффициентами, универсальный в следующем смысле: для каждого диофантова (перечислимого) множества
 свстоящего из упорядоченных наборов из пчисел, можно указать такое значение параметра т(номер множества
свстоящего из упорядоченных наборов из пчисел, можно указать такое значение параметра т(номер множества  ), что уравнение
), что уравнение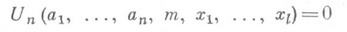
разрешимо относительно х 1, ..., xl тогда и только тогда, когда
 Существуют многочлены, универсальные в других смыслах (см., напр., [1]).
Существуют многочлены, универсальные в других смыслах (см., напр., [1]).Диофантовыми являются многие интересные с теоретико-числовой точки зрения множества, напр, множество всех простых чисел, множество всех совершенных чисел, множество всех тех п, для к-рых разрешимо уравнение Ферма

Доказательство теоремы о том, что перечислпмые множества диофантовы, является эффективным, т. е. для стандартно заданного перечислимого множества можно явно указать соответствующее диофантово уравнение. Этот универсальный метод, не использующий специфики рассматриваемых множеств, приводит к довольно громоздким многочленам, однако для нек-рых конкретных множеств удается найти их сравнительно простые диофантовы представления, опираясь, кроме перечислимости, на другие свойства этих множеств. Можно рассматривать и называть диофантовыми множества, представимые как множества всех тех упорядоченных наборов из пэлементов нек-рого кольца K, для к-рых в этом кольце разрешимо относительно х 1 , ..., xl уравнение вида (*), где Р - многочлен либо с целочисленными коэффициентами, либо с коэффициентами из К.
Лит.:[1] Матиясевич Ю. В., "Успехи матем. наук", 1972, т. 27, в. 5, с. 185-222.
Ю. В. Матиясевич.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
