АЛГЕБРАИЧЕСКАЯ ГРУППА

группа G, наделенная структурой алгебраического многообразия, в к-рой умножение и переход к обратному элементу являются регулярными отображениями (морфизмами) алгебраич. многообразий. А. г. наз. определенной над полем , если ее алгебраич. многообразие, а также морфизм и определены над В этом случае множество -рациональных точек многообразия Gявляется абстрактной группой, к-рая обозначается . А. г. наз. связной, если ее алгебраич. многообразие связно. Размерностью А. г. наз. размерность ее алгебраич. многообразия. В дальнейшем рассматриваются только связные А. г. Подгруппа H А. г. G наз. алгебраической, если она является замкнутым подмногообразием алгебраич. многообразия G. Для таких подгрупп пространство классов смежности (левых или правых) может быть естественным образом наделено структурой алгебраич. многообразия, обладающей универсальным свойством (см. Фактор-пространство алгебраической группы). Если подгруппа H, кроме того, нормальна, то факторгруппа является А. г. относительно указанной выше структуры; она наз. алгебраической факторгруппой. Гомоморфизм 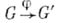А. г. наз. алгебраическим, если - морфизм их алгебраич. многообразий; если 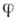определен над , то он наз. -гомоморфизмом. Аналогично определяется k- изоморфизм А. г.

Примеры А. г.: полная линейная группа - группа всех обратимых матриц порядка пс коэффициентами в фиксированном алгебраически замкнутом поле k, группа треугольных матриц, эллиптическая кривая.

Существуют два основных типа А. г., совершенно различных по своим свойствам: абелевы многообразия и линейные алгебраические группы;при этом принадлежность А. г. к одному из этих типов определяется исключительно свойствами многообразия группы. А. г. наз. абелевым многообразием, если ее алгеб-раич. многообразие полное. А. г. наз. линейной А. г., если она изоморфна алгебраич. подгруппе полной линейной группы. А. г. является линейной тогда и только тогда, когда ее алгебраич. многообразие аффинно. Эти два класса А. г. имеют тривиальное пересечение: если А. г. есть одновременно абелево многообразие и линейная группа, то она единичная группа. Изучение произвольных А. г. в значительной степени сводится к изучению абелевых многообразий и линейных групп. Именно, в произвольной А. г. существует единственная нормальная линейная алгебраич. подгруппа Нтакая, что факторгруппа G/Hесть абелево многообразие. Многочисленные примеры А. г., не являющихся ни линейными А. г., ни абелевыми многообразиями, дает теория обобщенных Якоби многообразий для алгебраич. кривых с особенностями (см. [4]). Естественное расширение класса алгебраич. групп приводит к понятию групповой схемы.