ЯКОБИ МНОГОЧЛЕНЫ — многочлены, ортогональные на отрезке [ 1, 1] с весовой функцией Стандартизованные Я. м. определяются Рoдрига фoрмулой а ортонормированные Я. м. имеют вид Многочлен удовлетворяет дифференциальному уравнению При и для ортонормированных Я. м. имеет… … Математическая энциклопедия
Якоби Карл Густав Якоб — Якоби (Jacobi) Карл Густав Якоб (10.12.1804, Потсдам, ‒ 18.2.1851, Берлин), немецкий математик, член Берлинской АН (1836), член корреспондент (1830) и почётный член (1833) Петербургской АН. Брат Б. С. Якоби. Один из создателей теории… … Большая советская энциклопедия
Якоби — I Якоби Борис Семенович (Мориц Герман) (21.9.1801, Потсдам, 11.3.1874, Петербург), русский физик и изобретатель в области электротехники, академик Петербургской АН (1847; член корреспондент 1838). Учился в Берлинском и Гёттингенском… … Большая советская энциклопедия
Многочлены Чебышёва — две последовательности многочленов Tn(x) и Un(x), названные в честь Пафнутия Львовича Чебышёва. Многочлены Чебышёва играют важную роль в теории приближений, поскольку корни многочленов Чебышёва первого рода используются в качестве узлов в… … Википедия
Многочлены Эрмита — Многочлены Эрмита определённого вида последовательность многочленов одной вещественной переменной. Многочлены Эрмита возникают в теории вероятностей, в комбинаторике, физике. Эти многочлены названы в честь Шарля Эрмита. Содержание 1… … Википедия
Многочлены Полачека — Многочлены Полачека последовательность многочленов , которые были рассмотрены Полачеком в 1950 году. Рекурсивное определение … Википедия
Многочлены Якоби — Полиномы Якоби класс ортогональных полиномов. Названы в честь Карла Густава Якоба Якоби. Ортогональные полиномы Якоби Открыты Якоби, Карл Густав Якоб Формула … Википедия
Многочлены Чебышева — Многочлены Чебышева две последовательности ортогональных многочленов и , названные в честь Пафнутия Львовича Чебышева. Многочлены Чебышева играют важную роль в теории приближений, поскольку корни многочленов Чебышева первого рода… … Википедия
Многочлены Лежандра — Многочлен Лежандра многочлен, который в наименьшей степени отклоняется от нуля в смысле среднего квадратического. Образует ортогональную систему многочленов, на отрезке по мере Лебега. Многочлены Лежандра могут быть получены из многочленов… … Википедия
Многочлены Лагерра — В математике, Многочлены Лагерра, названные в честь Эдмона Лагерра (1834 1886), являются каноническими решениями Уравнения Лагерра: являющегося линейным дифференциальным уравнением второго порядка. Многочлены Лагерра также используются в… … Википедия
Я. м. ортогональны на отрезке [—1,1] относительно веса (1—х)α (1 + х)β (см. Ортогональные многочлены). Введены К. Якоби (опубликовано в 1859). Частными случаями Я. м. являются многочлены Лежандра (при α = β = 0), многочлены Чебышева первого рода (при α = β = —1/2) и второго рода (при α = β = 1/2), ультрасферические многочлены (при α = β). В свою очередь Я. м. являются частным случаем гипергеометрической функции (См. Гипергеометрические функции). Дифференциальное уравнение для у = Pn (α,β)(х):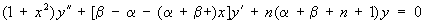
.