- Несобственные интегралы
-
обобщение классического понятия интеграла на случай неограниченных функций и функций, заданных на бесконечном промежутке интегрирования (см. Интеграл). Определённый интеграл как предел интегральных сумм Римана может существовать (иметь определённое конечное значение) лишь для ограниченных функций, заданных на конечном интервале. Поэтому, если интервал интегрирования или подынтегральная функция не ограничены, для определения интеграла требуется ещё один предельный переход: получающиеся при этом интегралы называются несобственными интегралами.Если функция f (x) интегрируема на любом конечном отрезке [a, N] и если существует
 то его называют Н. п. функции f (x) на интервале [а, ∞] и обозначают
то его называют Н. п. функции f (x) на интервале [а, ∞] и обозначают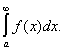 В этом случае говорят, что Н. и. сходится. Когда этот предел, а значит и Н. и., не существует, то иногда говорят, что Н. и. расходится. Например,
В этом случае говорят, что Н. и. сходится. Когда этот предел, а значит и Н. и., не существует, то иногда говорят, что Н. и. расходится. Например,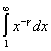 сходится при γ > 1 и расходится при γ ≤ 1. Аналогично определяют Н. и. на интервалах[—∞, b] и [—∞, ∞].Если функция f (x), заданная на отрезке [a, b], не ограничена в окрестности точки a, но интегрируема на любом отрезке [а + ε, b], 0 < ε < b - a и если существует
сходится при γ > 1 и расходится при γ ≤ 1. Аналогично определяют Н. и. на интервалах[—∞, b] и [—∞, ∞].Если функция f (x), заданная на отрезке [a, b], не ограничена в окрестности точки a, но интегрируема на любом отрезке [а + ε, b], 0 < ε < b - a и если существует то его называют Н. и. функции f (x) на [а, b] и записывают обычным образом:
то его называют Н. и. функции f (x) на [а, b] и записывают обычным образом: Аналогично поступают, если f (x) не ограничена в окрестности точки b.Если существует Н. и.
Аналогично поступают, если f (x) не ограничена в окрестности точки b.Если существует Н. и.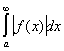 или
или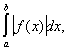 то говорят, что Н. и.
то говорят, что Н. и.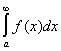 или
или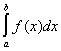 абсолютно сходится: если же последние интегралы сходятся (но первые расходятся), то Н. и.
абсолютно сходится: если же последние интегралы сходятся (но первые расходятся), то Н. и.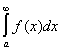 или
или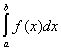 называются условно сходящимися.Задачи, приводящие к Н. и., рассматривались в геометрической форме Э. Торричелли и П. Ферма в 1644. Точные определения Н. и. даны О. Коши в 1823. Различие условно и абсолютно сходящихся Н. и. установлено Дж. Стоксом и П. Г. Л. Дирихле (1854). Ряд работ математиков 19 в. посвящен вычислению Н. и. в случаях, когда соответствующая первообразная не выражается через элементарные функции. Основными приемами вычисления Н. и. являются дифференцирование и интегрирование по параметру, разложение в ряды, применение теории вычетов. Значения многих Н. и. приводятся в различных таблицах.Н. и. имеют важное значение во многих областях математического анализа и его приложений. В теории специальных функций (цилиндрических функций, ортогональных многочленов и др.) одним из основных способов изучения является изображение функций в виде Н. и., зависящих от параметра, например
называются условно сходящимися.Задачи, приводящие к Н. и., рассматривались в геометрической форме Э. Торричелли и П. Ферма в 1644. Точные определения Н. и. даны О. Коши в 1823. Различие условно и абсолютно сходящихся Н. и. установлено Дж. Стоксом и П. Г. Л. Дирихле (1854). Ряд работ математиков 19 в. посвящен вычислению Н. и. в случаях, когда соответствующая первообразная не выражается через элементарные функции. Основными приемами вычисления Н. и. являются дифференцирование и интегрирование по параметру, разложение в ряды, применение теории вычетов. Значения многих Н. и. приводятся в различных таблицах.Н. и. имеют важное значение во многих областях математического анализа и его приложений. В теории специальных функций (цилиндрических функций, ортогональных многочленов и др.) одним из основных способов изучения является изображение функций в виде Н. и., зависящих от параметра, например (см. Гамма-функция). К Н. и. относится и Фурье интеграл, а также интегралы, встречающиеся при др. интегральных преобразованиях. Решения краевых задач (См. Краевые задачи) математической физики записываются кратными Н. и. с неограниченной подинтегральной функцией. В теории вероятностей важное значение имеет Н. и.
(см. Гамма-функция). К Н. и. относится и Фурье интеграл, а также интегралы, встречающиеся при др. интегральных преобразованиях. Решения краевых задач (См. Краевые задачи) математической физики записываются кратными Н. и. с неограниченной подинтегральной функцией. В теории вероятностей важное значение имеет Н. и.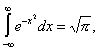 в теории диффракции света — Н. и.
в теории диффракции света — Н. и. В ряде случаев расходящимся Н. и. можно приписать определённое значение (см. Суммирование). В частности, если интеграл
В ряде случаев расходящимся Н. и. можно приписать определённое значение (см. Суммирование). В частности, если интеграл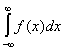 расходится, но существует
расходится, но существует то А называется главным значением Н. и. и обозначают
то А называется главным значением Н. и. и обозначают Так,
Так, Аналогично вводится главное значение Н. и. от неограниченных функций. В работах Н. И. Мусхелишвили и его учеников построена теория интегральных уравнений, содержащих Н. и., понимаемые в смысле главного значения.Лит.: Смирнов В. И., Курс высшей математики, 20 изд., т. 2, М. — Л., 1967; Фихтенгольц Г. М., Курс дифференциального и интегрального исчисления, 7 изд. т. 2, М., 1969; Кудрявцев Л. Д., Математический анализ, т. 1, М., 1970.
Аналогично вводится главное значение Н. и. от неограниченных функций. В работах Н. И. Мусхелишвили и его учеников построена теория интегральных уравнений, содержащих Н. и., понимаемые в смысле главного значения.Лит.: Смирнов В. И., Курс высшей математики, 20 изд., т. 2, М. — Л., 1967; Фихтенгольц Г. М., Курс дифференциального и интегрального исчисления, 7 изд. т. 2, М., 1969; Кудрявцев Л. Д., Математический анализ, т. 1, М., 1970.
Большая советская энциклопедия. — М.: Советская энциклопедия. 1969—1978.
