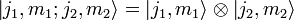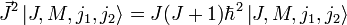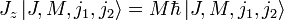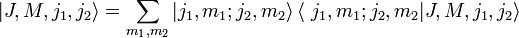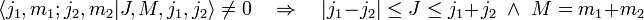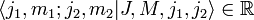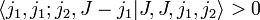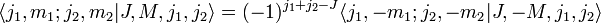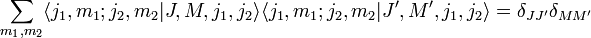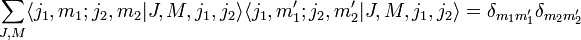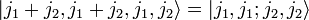- Коэффициенты Клебша-Гордана
-
Коэффициенты Клебша-Гордана
Коэффициенты Клебша-Гордана находят применение при описании взаимодействия квантовомеханических моментов импульса. Они представляют собой коэффициенты разложения собственных функций суммарного момента импульса по базису собственных функций суммируемых моментов импульса. Коэффициенты Клебша-Гордана применяются при вычислении спин-орбитального взаимодействия, а также в формализме изоспина.
Коэффициенты Клебша-Гордана названы в честь Альфреда Клебша (1833—1872) и Пауля Альберта Гордана (1837—1912).
Содержание
Взаимодействие моментов импульса
см. также статью Оператор момента импульса.
Рассмотрим два момента импульса J1 и J2, которые обладают квантовыми числами j1 и m1 (z-компонента) и j2 и m2. При этом m1 и m2 принимают значения m1 = [ − j1,...,j1] и m2 = [ − j2,...,j2] соответственно. Моменты импульса коммутируют [J1,J2] = 0, что означает, что оба могут быть измерены одновременно с любой точностью. Каждому моменту импульса соответствует свой базис собственных функций (векторов):
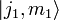 или
или 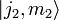 . В базисе
. В базисе 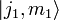 момент J1 принимает простой диагональный вид, аналогично J2 в базисе
момент J1 принимает простой диагональный вид, аналогично J2 в базисе 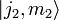 .
.При взаимодействии, оба момента импульса J1 и J2 складываются в общий момент
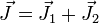 , который обладает квантовыми числами J и M, принимающими следующие значения
, который обладает квантовыми числами J и M, принимающими следующие значения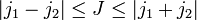 и M = [ − J,...,J] (с шагом 1).
и M = [ − J,...,J] (с шагом 1).
Так как суммарный момент импульса состоит из двух отдельных моментов импульса J1 и J2, то он может быть разложен в пространстве произведения двух собственных пространств отдельных моментов:
Однако вектора этого базиса не будут являться собственными векторами суммарного момента импульса
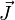 и его представление в этом базисе не будет иметь простой диагональной формы.
и его представление в этом базисе не будет иметь простой диагональной формы.Базис собственных векторов суммарного момента импульса
Собственные вектора момента
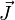 однозначно определяются квантовыми числами J, M, j1 и j2. В базисе этих векторов суммарный момент J принимает простую диагональную форму. А именно
однозначно определяются квантовыми числами J, M, j1 и j2. В базисе этих векторов суммарный момент J принимает простую диагональную форму. А именноКоэффициенты Клебша-Гордана дают переход путём унитарного преобразования от базиса произведения собственных пространств отдельных моментов
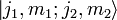 в базис собственных векторов
в базис собственных векторов 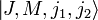 .
.Здесь
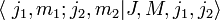 являются коэффициентами Клебша-Гордана.
являются коэффициентами Клебша-Гордана.Свойства коэффициентов Клебша-Гордана
- Коэффициенты Клебша-Гордана равны нулю, если не выполнено одно из двух условий
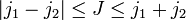 и M = m1 + m2:
и M = m1 + m2:
- Коэффициенты Клебша-Гордана задают действительными числами:
- Коэффициент Клебша-Гордана при M = J задают положительным:
- Коэффициенты Клебша-Гордана равны по модулю при M = − M:
- Коэффициенты Клебша-Гордана удовлетворяют условию ортогональности:
- Коэффициенты Клебша-Гордана удовлетворяют условию ортогональности:
Вычисление коэффициентов Клебша-Гордана
Собственное состояние с J = j1 + j2 и M = J непосредственно получается в базисе произведения собственных пространств составляющих моментов (только один коэффициент равен 1, остальные нулю)
Применением оператора уменьшения
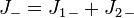 можно получить состояния от
можно получить состояния от 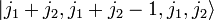 до
до 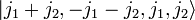 , или же все состояния с J = j1 + j2 и M = − J,...,J = − j1 − j2,...,j1 + j2.
, или же все состояния с J = j1 + j2 и M = − J,...,J = − j1 − j2,...,j1 + j2.Состояние
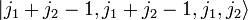 можно получить из условия ортогональности к состоянию
можно получить из условия ортогональности к состоянию 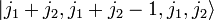 и соглашению о том, что коэффициент Клебша-Гордана при M = J является положительным.
и соглашению о том, что коэффициент Клебша-Гордана при M = J является положительным.Применением оператора уменьшения к J = j1 + j2 − 1 можно опять получить все состояния с M = − j1 − j2 + 1,...,j1 + j2 − 1. Итеративно можно применять эту процедуру для всех J до J = | j1 − j2 | .
См. также
Ссылки
Таблица с примерами для некоторых значений j1 и j2 (PDF, 70 kB)
Литература
- Собельман И. И.: Введение в теорию атомных спектров. Издательство Литература. 1963
Wikimedia Foundation. 2010.
Коэффициенты Клебша — Коэффициенты Клебша Гордана находят применение при описании взаимодействия квантовомеханических моментов импульса. Они представляют собой коэффициенты разложения собственных функций суммарного момента импульса по базису собственных функций… … Википедия
КЛЕБША - ГОРДАНА КОЭФФИЦИЕНТЫ — возникают в квантовой механике при решении задачи сложения моментов (орбитальных, спиновых или полных) независимых частиц (или систем), а также при сложении изотопических спинов и вообще любых аналогичных величин, связанных с группами SU(2 )и… … Физическая энциклопедия
РАКА КОЭФФИЦИЕНТЫ — в квантовой механике характеризуют сложение трёх (и более) угл. моментов, а также изотопических спинов и др. аналогичных величин, связанных с группой трёхмерных вращений (см. Квантовое сложение моментов). Введены Дж. Рака (G. Racah, 1942) при… … Физическая энциклопедия
Теорема Вигнера — Теорема Вигнера Эккарта теорема из теории представлений и квантовой механики. В ней говорится, что матричный элемент сферического оператора операторов в базисе собственных функций оператора углового момента может быть представлен в… … Википедия
3j символ — 3 j символы Вигнера, называемые также 3 jm символами, находят применение в квантовой механике и связаны с коэффициентами Клебша Гордана следующими формулами: Содержание 1 Обратная связь … Википедия
6-j символ — 6 j символы Вигнера введены в обращение Юджином Вигнером в 1940, и опубликованы в 1965. Понятие 6 j символа возникает при квантовомеханическом сложении трёх моментов импульса, а именно, три угловых момента можно сложить тремя способами (типами… … Википедия
Клебш, Альфред — Рудольф Фридрих Альфред Клебш Rudolf Friedrich Alfred Clebsch Дата рождения … Википедия
Клебш, Рудольф Фридрих Альфред — Альфред Клебш Рудольф Фридрих Альфред Клебш (нем. Rudolf Friedrich Alfred Clebsch; 19 января 1833, Кёнигсберг 7 ноября 1872, Гёттинген) немецкий математик, ученик Гессе и Неймана. В 1858 был профессором политехнической школы в Карлсруэ, затем в … Википедия
Клебш — Клебш, Рудольф Фридрих Альфред Альфред Клебш Рудольф Фридрих Альфред Клебш (нем. Rudolf Friedrich Alfred Clebsch; 19 января 1833, Кёнигсберг 7 ноября 1872, Гёттинген) немецк … Википедия
Клебш, Фридрих — Альфред Клебш Рудольф Фридрих Альфред Клебш (нем. Rudolf Friedrich Alfred Clebsch; 19 января 1833, Кёнигсберг 7 ноября 1872, Гёттинген) немецкий математик, ученик Гессе и Неймана. В 1858 был профессором политехнической школы в Карлсруэ, затем в … Википедия