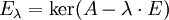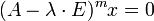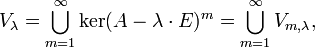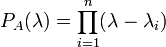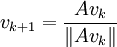- Корневое подпространство
-
 Красным цветом обозначен собственный вектор. Он, в отличие от синего, при деформации не изменил направление и длину, поэтому является собственным вектором, соответствующим собственному значению λ = 1. Любой вектор, параллельный красному вектору, также будет собственным, соответствующим тому же собственному значению. Множество всех таких векторов (вместе с нулевым) образует собственное подпространство.
Красным цветом обозначен собственный вектор. Он, в отличие от синего, при деформации не изменил направление и длину, поэтому является собственным вектором, соответствующим собственному значению λ = 1. Любой вектор, параллельный красному вектору, также будет собственным, соответствующим тому же собственному значению. Множество всех таких векторов (вместе с нулевым) образует собственное подпространство.Содержание
Определения собственного числа, собственного и корневого вектора линейного оператора
Пусть L — линейное пространство над полем K,
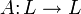 — линейное преобразование.
— линейное преобразование.Собственным вектором линейного преобразования A называется такой ненулевой вектор
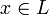 , что для некоторого
, что для некоторого 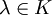
- Ax = λx
Собственным значением линейного преобразования A называется такое число
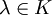 , для которого существует собственный вектор, то есть уравнение Ax = λx имеет ненулевое решение
, для которого существует собственный вектор, то есть уравнение Ax = λx имеет ненулевое решение 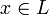 .
.Собственным подпространством линейного преобразования A для данного собственного числа
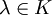 называется множество всех собственных векторов
называется множество всех собственных векторов 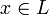 , соответствующих данному собственному числу (дополненное нулевым вектором). Обозначим его Eλ. По определению,
, соответствующих данному собственному числу (дополненное нулевым вектором). Обозначим его Eλ. По определению,где E — единичный оператор.
Корневым вектором линейного преобразования A для данного собственного значения
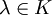 называется такой ненулевой вектор
называется такой ненулевой вектор 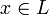 , что для некоторого натурального числа m
, что для некоторого натурального числа mЕсли m является наименьшим из таких натуральных чисел (то есть
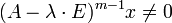 ), то m называется высотой корневого вектора x.
), то m называется высотой корневого вектора x.Корневым подпространством линейного преобразования A для данного собственного числа
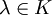 называется множество всех корневых векторов
называется множество всех корневых векторов 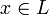 , соответствующих данному собственному числу (дополненное нулевым вектором). Обозначим его Vλ. По определению,
, соответствующих данному собственному числу (дополненное нулевым вектором). Обозначим его Vλ. По определению,где

Свойства собственных значений, собственных и корневых векторов и пространств
Общий случай
Подпространство
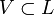 называется инвариантным подпространством линейного преобразования A (A-инвариантным подпространством), если
называется инвариантным подпространством линейного преобразования A (A-инвариантным подпространством), если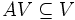 .
.
- Собственные подпространства Eλ, корневые подпространства Vλ и подпространства Vm,λ линейного оператора A являются A-инвариантными.
- Собственные векторы являются корневыми (высоты 1):
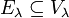 ;
;
- Корневые векторы могут не быть собственными: например, для преобразования двумерного пространства, заданного матрицей
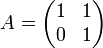
- (A − 1)2 = 0, и все векторы являются корневыми, соответствующими собственному числу 1, но A имеет единственный собственный вектор (с точностью до умножения на число).
- Для разных собственных значений корневые (и, следовательно, собственные) подпространства имеют тривиальное (нулевое) пересечение:
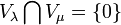 если
если 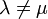 .
.
Конечномерные линейные пространства
Выбрав базис в n-мерном линейном пространстве L, можно сопоставить линейному преобразованию
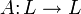 квадратную
квадратную 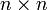 матрицу и определить для неё характеристический многочлен
матрицу и определить для неё характеристический многочлен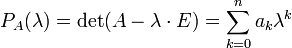 .
.
- Характеристический многочлен не зависит от базиса в L. Его коэффициенты являются инвариантами оператора A. В частности,
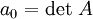 ,
,  не зависят от выбора базиса.
не зависят от выбора базиса. - Собственные значения, и только они, являются корнями характеристического многочлена матрицы.
- Количество различных собственных значений не может превышать размер матрицы.
Пусть числовое поле алгебраически замкнуто (например, является полем комплексных чисел). Тогда характеристический многочлен разлагается в произведение n линейных множителей
- где
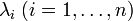 — собственные значения; некоторые из λi могут быть равны. Кратность собственного значения λi — это число множителей равных λ − λi в разложении характеристического многочлена на линейные множители (называется также алгебраическая кратность собственного значения).
— собственные значения; некоторые из λi могут быть равны. Кратность собственного значения λi — это число множителей равных λ − λi в разложении характеристического многочлена на линейные множители (называется также алгебраическая кратность собственного значения).
- Размерность корневого пространства
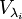 равна кратности собственного значения.
равна кратности собственного значения. - Векторное пространство L разлагается в прямую сумму корневых подпространств (по теореме о жордановой форме):

- где суммирование производится по всем λi — собственным числам A.
- Геометрическая кратность собственного значения λi — это размерность соответствующего собственного подпространства
 ; геометрическая кратность собственного значения не превосходит его кратности, поскольку
; геометрическая кратность собственного значения не превосходит его кратности, поскольку 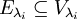
Гильбертовы пространства над полем комплексных чисел и нормальные операторы
Наличие скалярного произведения позволяет выделить важные классы операторов, собственные значения и собственные векторы которых обладают рядом дополнительных полезных свойств.
Нормальным оператором называется оператор A, коммутирующий со своим сопряжённым A * :
- AA * = A * A.
Частными классами нормальных операторов являются самосопряжённые (эрмитовы) операторы (A = A * ), антиэрмитовы операторы (A = − A * ) и унитарные операторы (A − 1 = A * ), а также их вещественные варианты: симметричные операторы, антисимметричные операторы и ортогональные преобразования.
- Все корневые векторы нормального оператора являются собственными.
- Собственные векторы нормального оператора A, соответствующие различным собственным значениям, ортогональны. То есть если Ax = λx, Ay = μy и
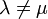 , то (x,y) = 0. (Для произвольного оператора это неверно.)
, то (x,y) = 0. (Для произвольного оператора это неверно.)
- Все собственные значения самосопряжённого оператора являются вещественными.
- Все собственные значения антиэрмитового оператора являются мнимыми.
- Все собственные значения унитарного оператора лежат на единичной окружности | λ | = 1.
- В конечномерном случае, сумма размерностей собственных подпространств нормального оператора
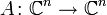 , соответствующих всем собственным значениям, равна размерности матрицы, а векторное пространство разлагается в ортогональную сумму собственных подпространств:
, соответствующих всем собственным значениям, равна размерности матрицы, а векторное пространство разлагается в ортогональную сумму собственных подпространств:
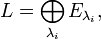
- где суммирование производится по всем λi — собственным числам A, а
 взаимно ортогональны для различных λi.
взаимно ортогональны для различных λi.
- Последнее свойство для нормального оператора над
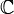 является характеристическим: оператор нормален тогда и только тогда, когда его матрица имеет диагональный вид в каком-нибудь ортонормированном базисе (в конечномерном случае).
является характеристическим: оператор нормален тогда и только тогда, когда его матрица имеет диагональный вид в каком-нибудь ортонормированном базисе (в конечномерном случае).
Положительные матрицы
Квадратная вещественная
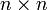 матрица A = (aij) называется положительной, если все её элементы положительны: aij > 0.
матрица A = (aij) называется положительной, если все её элементы положительны: aij > 0.Теорема Перрона (частный случай теоремы Перрона-Фробениуса): Положительная квадратная матрица A имеет положительное собственное значение r, которое имеет алгебраическую кратность 1 и строго превосходит абсолютную величину любого другого собственного значения этой матрицы. Собственному значению r соответствует собственный вектор er, все координаты которого строго положительны. Вектор er — единственный собственный вектор A (с точностью до умножения на число), имеющий неотрицательные координаты.
Собственный вектор er может быть вычислен посредством прямых итераций: выберем произвольный начальный вектор v0 с положительными координатами. Положим:
Последовательность vk сходится к нормированному собственному вектору
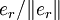 .
.Другая область применения метода прямых итераций — поиск собственных векторов положительно определённых симметричных операторов.
Литература
- Гантмахер Ф. Р. Теория матриц. — М.: Наука, 1966. — 576 с.
- Уилкинсон Д. Х. Алгебраическая проблема собственных значений. — М.: Наука, 1970. — 564 с.
Wikimedia Foundation. 2010.