КОРНЕВОЙ ВЕКТОР

линейного преобразования Авекторного пространства Vнад полем k - вектор 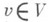, лежащий в ядре линейного преобразования 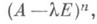где п - целое положительное число, зависящее от Аи v. Число l будет непременно собственным значением преобразования A. Если при этом 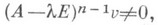то говорят, что v - К. в. высоты п, принадлежащей l.

Понятие К. в. обобщает понятие собственного вектора преобразования А:собственные векторы - это в точности К. в. высоты 1. Множество V_lK. в., принадлежащих фиксированному собственному значению l, является линейным подпространством в V, инвариантным относительно А. Оно наз. корневым подпространством, принадлежащим собственному значению К. К. в., принадлежащие различным собственным значениям, линейно независимы; в частности, если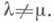

Пусть Vконечномерно. Если все корни характери-стич. многочлена преобразования Алежат в k(напр., когда kалгебраически замкнуто), то Vраскладывается в прямую сумму различных корневых подпространств:

Это разложение является частным случаем весового разложения векторного пространства Vотносительно расщепляемой нильпотентной алгебры Ли Lлинейных преобразований: алгеброй Lв этом случае служит одномерная подалгебра, порожденная преобразованием Ав алгебре Ли всех линейных преобразований пространства V(см. Вес представления).

Если в нек-ром базисе матрица преобразования Аявляется жордановой матрицей, то компоненты разложения (*) могут быть описаны следующим образом: корневое подпространство V_l, есть линейная оболочка множества тех векторов базиса, к-рые отвечают жордановым клеткам с собственным числом l.

Лит.:[1] Воеводин В. В., Линейная алгебра, М., 1974; [2] М а л ь ц е в А. И., Основы линейной алгебры, 3 изд., М., 1970. В. Л. Попов.