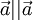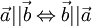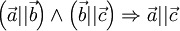Коллинеарные вектора

Два вектора называются коллинеа́рными, если они лежат на параллельных прямых или на одной прямой. Допусти́м, но не рекомендуется, синоним — «параллельные» векторы. Коллинеарные векторы могут быть одинаково направлены («сонаправлены») или противоположно направлены (в последнем случае их иногда называют «антиколлинеарными» или «антипараллельными»).

Обозначения

• Коллинеарные векторы: $\vec{a}||\vec{b}$
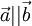
• Сонаправленные векторы: $\vec{a}\uparrow\uparrow\vec{b}$
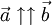
• Противоположно направленные векторы: $\vec{a}\uparrow\downarrow\vec{b}$

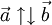
Свойства коллинеарности

Пусть 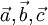$\vec{a},\vec{b},\vec{c}$ — векторы пространства $\mathbb{R}^n$. Тогда верны следующие утверждения:

• Коллинеарность — отношение эквивалентности, то есть оно:
  1. рефлексивно: $\vec{a}||\vec{a}$
  2. симметрично: $\vec{a}||\vec{b}\Leftrightarrow\vec{b}||\vec{a}$
  3. транзитивно: $\left(\vec{a}||\vec{b}\right)\land\left(\vec{b}||\vec{c}\right)\Rightarrow\vec{a}||\vec{c}$
• Нулевой вектор коллинеарен любому вектору: $\vec{a}||\vec{0}$
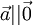
• Скалярное произведение коллинеарных векторов 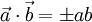$\vec{a}\cdot\vec{b} = \pm a b$ равно произведению длин векторов (взятых со знаком «-», если векторы противоположно направлены)
• Векторное произведение коллинеарных векторов $\vec{a}\times\vec{b} = 0$. Это критерий коллинеарности двух векторов.
• Коллинеарные векторы линейно зависимы. Это тоже критерий коллинеарности.
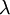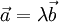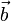• Существует действительное число $\;\lambda$ такое, что $\vec{a} = \lambda\vec{b}$ для коллинеарных $\vec{a}$ и $\vec{b}$, за исключением особого случая 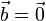$\vec{b}=\vec{0}$. Это переформулировка предыдущего свойства и тоже критерий коллинеарности.
• На плоскости 2 неколлинеарных вектора 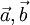$\vec{a},\vec{b}$ образуют базис. Это значит, что любой вектор 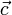$\vec{c}$ можно представить в виде: 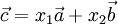$\vec{c}=x_1\vec{a}+x_2\vec{b}$. Тогда 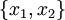$\;\{x_1, x_2\}$ будут координатами 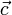$\vec{c}$ в данном базисе.

Другие объекты

Выше описанные критерии коллинеарности позволяют определить это понятие для векторов, понимаемых не в геометрическом смысле (а, например, как элементы произвольного линейного пространства).

Иногда коллинеарными называют те точки (или другие объекты), которые лежат на (принадлежат) одной прямой.

См. также

• Компланарность