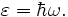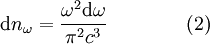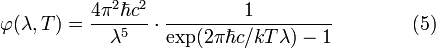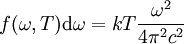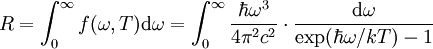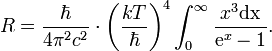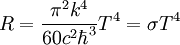Закон излучения Планка

Формула Планка — выражение для спектральной плотности мощности излучения абсолютно чёрного тела, которое было получено Максом Планком для равновесной плотности излучения u(ω,T). После того как вывод Релея — Джинса для излучения абсолютно чёрного тела, столкнулся с ультрафиолетовой катастрофой (расходимость при больших частотах), стало ясно, что классическая физика не в силах объяснить его излучение. Для вывода формулы Планк в 1900 году сделал предположение о том, что электромагнитное излучение испускается в виде отдельных порций энергии (квантов), величина которых связана с частотой излучения выражением:

$\varepsilon = \hbar \omega.$

По сути это было «рождение» фотона. Коэффициент пропорциональности 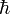$\hbar$ в последствии назвали постоянной Планка, 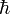$\hbar$ = 1.054 · 10^-34 Дж·с.

Вывод для абсолютно чёрного тела

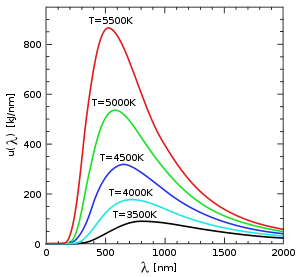Излучение абсолютно чёрного тела

Выражение для средней энергии колебания частотой ω дается выражением:

$\overline{\varepsilon} = \frac{\hbar \omega} {\mathrm{exp}( \hbar \omega / kT) -1} \qquad\qquad (1)$.

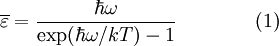Количество стоячих волн в трёхмерном пространстве равно:

$\mathrm{d}n_{\omega}= \frac{\omega^2 \mathrm{d} \omega}{\pi^2 c^3} \qquad\qquad (2)$

перемножив (1) и (2), получим плотность энергии, приходящуюся на интервал частот dω:

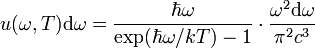$u(\omega,T)\mathrm{d} \omega = \frac{\hbar \omega} {\mathrm{exp}(\hbar \omega / kT) -1} \cdot \frac{\omega^2 \mathrm{d} \omega}{\pi^2 c^3}$ откуда:

$u(\omega,T)=\frac{\hbar \omega^3 }{\pi^2 c^3} \cdot \frac{1} {\mathrm{exp}(\hbar \omega / kT) -1} \qquad\qquad (3)$

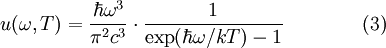
Зная связь испускательной способности абсолютно чёрного тела f(ω,T) с равновесной плотностью энергией теплового излучения 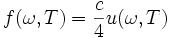$f(\omega,T)= \frac{c}{4} u(\omega,T)$, для f(ω,T) находим: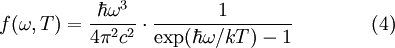

$f(\omega,T)=\frac{\hbar \omega^3 }{4 \pi^2 c^2} \cdot \frac{1} {\mathrm{exp}(\hbar \omega / kT) -1} \qquad\qquad (4)$

Выражения (3) и (4)носят название формулы Планка.

Испускательную способность АЧТ, выраженную через длину волны λ т.е. 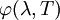$\varphi(\lambda, T)$ можно выразить используя соотношение:

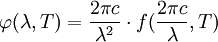$\varphi(\lambda, T)= \frac{2 \pi c}{\lambda^2} \cdot f(\frac{2 \pi c}{\lambda},T)$, получим

$\varphi(\lambda, T) = \frac{4\pi^2 \hbar c^2}{\lambda^5} \cdot \frac{1}{\mathrm{exp}(2 \pi \hbar c/ kT \lambda) -1} \qquad\qquad (5)$

Переход к формулам Релея—Джинса.

Формула Планка точно согласуется с экспериментальными данными во всём интервале частот от 0 до 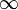$\infty$. При малых частотах (больших длинах волн), когда 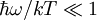$\hbar \omega / kT \ll 1$ можно разложить экспоненту по 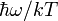$\hbar \omega / kT$. В результате получим, что 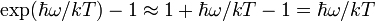$\mathrm{exp}(\hbar \omega / kT) -1 \approx 1 + \hbar \omega / kT -1 = \hbar \omega / kT$, тогда (3) и (4) переходят в формулу Релея—Джинса.

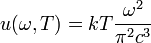$u(\omega,T) = kT \frac{\omega^2 }{\pi^2 c^3}$ и

$f(\omega,T) \mathrm{d} \omega = kT \frac{\omega^2 }{4 \pi^2 c^2}$

Переход к закону Стефана — Больцмана.

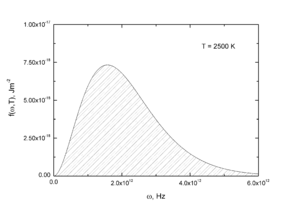
Энергетическая светимость равна площади, ограниченной графиком функции f(ω,Т)

Для энергетической светимости следует записать интеграл:

$R= \int_0^{\infty} f(\omega,T)\mathrm{d} \omega = \int_0^{\infty} \frac{\hbar \omega^3}{4 \pi^2 c^2} \cdot \frac{\mathrm{d} \omega }{\mathrm{exp}( \hbar \omega / kT) -1}$

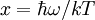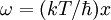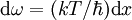Введём переменную $x = \hbar \omega / kT$, тогда $\omega = (kT/ \hbar)x$, $\mathrm{d} \omega = (kT/ \hbar) \mathrm{d}x$, получим

$R= \frac{\hbar}{4 \pi^2 c^2} \cdot \left( \frac{kT}{\hbar} \right)^4 \int_0^{\infty} \frac{x^3 \mathrm{d}\mathrm{x}}{\mathrm{e}^x -1}.$

Полученный интеграл имеет точное значение: 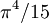$~\pi^4 / 15$, подставив его получим известный закон Стефана — Больцмана:

$R= \frac{\pi^2 k^4}{60 c^2 \hbar^3}T^4 = \sigma T^4$

Подстановка численных значений констант даёт значение для 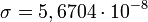$\sigma = 5,6704 \cdot 10^{-8}$ Вт/(м² $\cdot$ K⁴), что хорошо согласуется с экспериментом.

Переход к закону смещения Вина

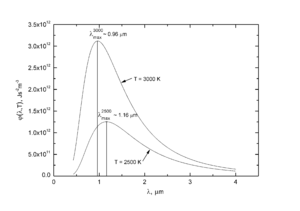
Для нахождения закона, по которому происходит смещение максимума φ(λ,Т) в зависимости от температуры, надо исследовать функцию φ(λ,Т) на максимум.

Для перехода к закону Вина, необходимо продифференцировать выражение (5) по λ и приравнять нулю (поиск экстремума):

$\frac{ \mathrm{d} \varphi(\lambda, T)}{\mathrm{d} \lambda} = \frac{ 4 \pi^2 \hbar c^2 \left\{ \frac{2 \pi \hbar c}{k T \lambda} \mathrm{exp} \left( \frac{2 \pi \hbar c}{k T \lambda} \right) - 5 \left[ \mathrm{exp} \left( \frac{2 \pi \hbar c}{k T \lambda} \right) -1 \right] \right\} } {\lambda^6 \left[ \mathrm{exp} \left( \frac{2 \pi \hbar c}{k T \lambda} \right) -1 \right]^2} =0$.

Значение λ_m, при котором функция достигает максимума, обращает в нуль выражение, стоящее в фигурных скобках. Обозначим 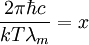$\frac{2 \pi \hbar c}{k T \lambda_m} = x$, получится уравнение:

$~xe^x-5(e^x-1)=0$.

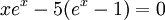Решение такого уравнение даёт x=4.965. Следовательно 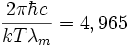$\frac{2 \pi \hbar c}{k T \lambda_m} = 4,965$, отсюда немедленно получается:

$T \lambda_m = \frac{2 \pi \hbar c}{4.965 k} = b$.

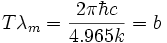Численная подстановка констант даёт значение для b, совпадающее с экспериментом.

Литература

• М. Планк. Об одном улучшении закона излучения Вина. Избранные научные труды. Русский пер. из сборника под ред. А.П. Виноградова. Стр.249 (http://dbserv.ihep.su/~elan/planckdisk/src/pl1900/rus.pdf )
• М. Планк. К теории распределения энергии излучения нормального спектра. Избранные научные труды. Русский пер. из сборника под ред. А.П. Виноградова. Стр.251 (http://dbserv.ihep.su/~elan/planckdisk/src/pl1900b/rus.pdf )
• Симулятор излучения абсолютно черного тела http://www.vias.org/simulations/simusoft_blackbody.html