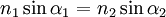Закон Снелиуса

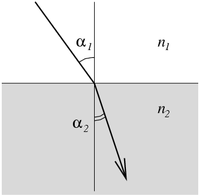Преломление света на границе двух сред с различным показателем преломления

Закон Снелла (Снеллиуса) преломления света описывает преломление света на границе двух сред. Также применим и для описания преломления волн другой природы, например звуковых.

Закон был открыт в начале XVII века голландским математиком Виллебрордом Снеллом, известным также под латинизированным именем Снеллиус.

Угол падения света на поверхность связан с углом преломления соотношением

$n_1 \sin \alpha_1 = n_2 \sin \alpha_2\,$

Здесь:

• n₁ — показатель преломления среды, из которой свет падает на границу раздела;
• α₁ — угол падения света — угол между падающим на поверхность лучом и нормалью к поверхности;
• n₂ — показатель преломления среды, в которую свет попадает, пройдя границу раздела;
• α₂ — угол преломления света — угол между прошедшим через поверхность лучом и нормалью к поверхности.

Если 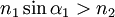$n_1 \sin \alpha_1 > n_2\,$, имеет место полное внутреннее отражение (преломлённый луч отсутствует, падающий луч полностью отражается от границы раздела сред)

• Следует заметить, что в случае анизотропных сред (например, кристаллов с низкой симметрией или механически деформированных твердых тел) преломление подчиняется несколько более сложному закону. При этом возможна зависимость направления преломленного луча не только от направления падающего, но и от его поляризации (см. двойное лучепреломление).

• Также следует заметить, что закон Снелла не описывает соотношение интенсивностей и поляризаций падающего, преломленного и отраженного лучей.

• Закон Снелла хорошо определен для случая «геометрической оптики», т.е. в случае, когда длина волны достаточно мала по сравнению с размерами преломляющей поверхности, вообще же говоря работает в рамках приближенного описания, каковым и является геометрическая оптика.

Теоретическое объяснение закона Снелла - см. в статье Преломление.

Ссылки

• БСЭ: Закон Снелла
• Элементы большой науки: Закон Снеллиуса