Теорема Паппа

Теоре́ма Па́ппа — это классическая теорема геометрии. Она формулируется следующим образом:

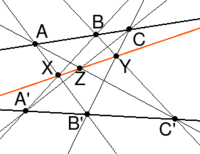
Пусть A, B, C — три точки на одной прямой, A' , B' , C'  — три точки на другой прямой. Пусть три прямые АВ' , BC' , CA' пересекают три прямые A’B, B’C, C’A, соответственно в точках X, Y, Z. Тогда точки X, Y, Z лежат на одной прямой.

Несложно видеть, что двойственная формулировка к теореме Паппа является лишь переформулировкой самой теоремы.

Пусть прямые $a_1,a_2,a_3$ проходят через точку A, $a_1',a_2',a_3'$ проходят через точку A'. $a_1$ пересекает $a_2'$ и $a_3'$ в точках B и C, a_2 пересекает $a_1'$ и $a_3'$ в точках C' и Z, $a_3$ пересекает $a_1'$ и $a_2'$ в точках B' и X. Тогда прямые BC', B’C и XZ пересекаются в одной точке (на чертеже — Y) или параллельны.

Теорема Паппа является вырожденным случаем в теореме Паскаля: если заменить в теореме Паскаля вписанный в конику шестиугольник на вписанный в пару пересекающихся прямых, то она станет эквиевалентной теореме Паппа. Сам Паскаль считал пару прямых коническим сечением (то есть считал теорему Паппа частным случаем своей теоремы).

История

Формулировка и доказательство этой теоремы содержатся в «Математическом собрании» Паппа Александрийского (начало IV века н. э.). В Новое время теорема была опубликована издателем и комментатором работ Паппа Федерико Коммандино в 1566 году.

Доказательство

Если увести на бесконечность прямую XY, то теорема переходит в несложное утверждение о параллельности прямых, проще всего доказываемое с применением гомотетии:

Пусть A, B, C — три точки на одной прямой, A' , B' , C'  — три точки на другой прямой, при этом AB' параллельно A’B, а BC' параллельно B’C. Тогда A’C параллельно AC'.

Ссылки

• Р.Курант, Г.Роббинс, Что такое математика? Глава IV, § 5.3.

Примечания