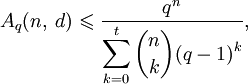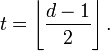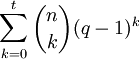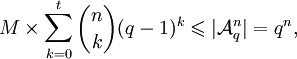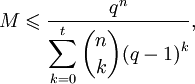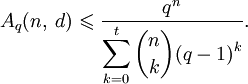Граница сферической упаковки

В теории кодирования грани́ца Хэ́мминга определяет пределы возможных значений параметров произвольного блокового кода. Также известна как граница сферической упаковки. Коды, достигающие границы Хэмминга, называют совершенными или плотноупакованными.

Формулировка

Пусть 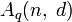$A_q(n,\;d)$ обозначает максимально возможную мощность q-чного блокового кода C длины n и минимального расстояния d (q-чный блоковый код длины n — это подмножество слов 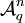$\mathcal{A}_q^n$ с алфавитом 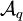$\mathcal{A}_q$, состоящим из q элементов).

Тогда

$A_q(n,\;d)\leqslant\frac{q^n}{\displaystyle\sum_{k=0}^t\binom{n}{k}(q-1)^k},$

где

$t=\left\lfloor\frac{d-1}{2}\right\rfloor.$

Доказательство

По определению d, если при передаче кодового слова случилось до 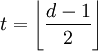$t=\left\lfloor\frac{d-1}{2}\right\rfloor$ ошибок, то с помощью декодирования, ограниченного минимальным расстоянием, мы будем способны безошибочно распознать посланное кодовое слово.

Для данного кодового слова 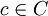$c\in C$, рассмотрим сферу радиуса t вокруг c. Благодаря тому, что данный код способен исправлять до 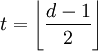$t=\left\lfloor\frac{d-1}{2}\right\rfloor$ ошибок, ни одна сфера не пересекается ни с какой другой и содержит

$\sum_{k=0}^t \binom{n}{k}(q-1)^k$

кодовых слов, так как мы можем позволить t (и менее) символам (из всех n символов слова) принять одно из (q − 1) возможных значений, отличных от значения соответствующего символа данного слова (вспомним, что сам код является q-чным).

Пусть M обозначает количество слов в C. Объединяя сферы вокруг всех кодовых слов, мы замечаем, что результирующее множество содержится в 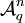$\mathcal{A}_q^n$. Так как сферы непересекающиеся, можно суммировать элементы каждой из них и получить

$M\times\sum_{k=0}^t\binom{n}{k}(q-1)^k\leqslant|\mathcal{A}_q^n|=q^n,$

откуда для любого кода C

$M\leqslant\frac{q^n}{\displaystyle\sum_{k=0}^t\binom{n}{k}(q-1)^k},$

а, значит,

$A_q(n,\;d)\leqslant\frac{q^n}{\displaystyle\sum_{k=0}^t\binom{n}{k}(q-1)^k}.$

Совершенные коды

Коды, достигающие границы Хэмминга, называют совершенными. Были открыты следующие типы совершенных кодов: коды Хэмминга и коды Голея. Имеются ещё тривиальные совершенные коды: двоичные коды с повторением нечётной длины, коды с одним кодовым словом и коды, включающие всё множество $F_q^n$.

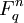Титвайненом и Ван Линтом было доказано, что любой нетривиальный совершенный код имеет параметры кода Хэмминга или кода Голея^[1][2].

Примечания

1. ↑ Tietavainen A., Perko A. There are no unknown perfect binary codes. — Annales Universitatis Turkuensis. — Ser. A, I 148, 3-10[6], 1971.
2. ↑ Lint van J. H. Nonexistence theorems for perfect error-correcting codes. — Computers in Algebra and Number Theory. — Vol. IV [6], 1971.

Литература

• MacWilliams F. J. and Sloane N. J. A. The Theory of Error-Correcting Codes. — Amsterdam, Netherlands, North-Holland, § 1.5, § 6.8, 1977.
• Blahut Richard E. Theory and Practice of Error-Control Codes. — Addison-Wesley publishing company, 1984. Есть перевод издательства «Мир»: Блейхут Р. «Теория и практика кодов контролирующих ошибки».

См. также

• Граница Синглтона
• Неравенство Гильберта — Варшамова
• Граница Плоткина
• Граница Джонсона