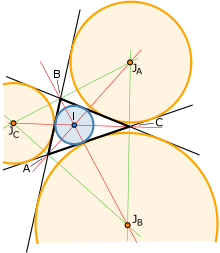
Вневписанная окружность

Вписанная (с центром I) и 3 вневписанные (с центрами в J) окружности в $\Delta ABC$

Вневпи́санная окружность треугольника — окружность, касающаяся одной из сторон треугольника и продолжений двух других его сторон. Таких окружностей, в отличие от вписанной, для любого треугольника существует ровно 3.

Существование и единственность вневписанной окружности обусловлено тем, что биссектрисы двух внешних углов треугольника и биссектриса внутреннего угла, не смежного с этими двумя, пересекаются в одной точке, которая и является центром такой окружности.

Свойства

Здесь используются обозначения: $r_1, r_2, r_3$ — радиусы вневписанных окружностей с центрами $I_1, I_2, I_3$, касающиеся соответственно сторон $a, b, c$ треугольника; p — полупериметр треугольника; r — радиус вписанной окружности; R — радиус описанной окружности.

• Длина отрезка касательной, проведенной к вневписанной окружности из противоположной вершины, равна полупериметру треугольника.
• Площадь треугольника $S=r_1(p-a)=r_2(p-b)=r_3(p-c)=\frac{r_1r_2r_3}{p}=\sqrt{rr_1r_2r_3}$
• $\frac{1}{r}=\frac{1}{r_1}+\frac{1}{r_2}+\frac{1}{r_3}$
• $4R=r_1+r_2+r_3-r$
• исходный треугольник является ортотреугольником $\Delta I_1I_2I_3$
• барицентрические координаты $I_1=(-a,b,c)$
• Формула Эйлера для вневписанных окружностей: $OI_i^2=R^2+2Rr_i$, где O — центр описанной окружности.
• $r_1r_2=p(p-c); rr_1=(p-b)(p-c)$
• Радикальный центр вневписанных окружностей — точка Шпикера (центр вписанной окружности срединного треугольника).
• Центры вписанной и вневписанных окружностей — неподвижные точки изогонального сопряжения.
• Центр окружности, проходящей через центры вневписанных окружностей — точка Бевэна.
• Если треугольник вписан в эллипс, фокус которого лежит на стороне этого треугольника, то вневписанная окружность касается этой стороны в фокусе.

Литература

• Понарин Я. П. Элементарная геометрия. В 2 тт. — М.: МЦНМО, 2004. — С. 44-48. — ISBN 5-94057-170-0

См. также

• Вписанная окружность
• Описанная окружность
• Теорема Мансиона
• Теорема Фейербаха