Векторно-векторное произведение векторов
- Векторно-векторное произведение векторов
-
Тройно́е ве́кторное произведе́ние (другое название: двойное векторное произведение) ![\left[ \vec{a}, \vec{b}, \vec{c} \right]](/pictures/wiki/files/48/0e6a64ecd01d00a9fa21e04ac4c4f468.png) векторов
векторов 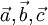 — векторное произведение вектора
— векторное произведение вектора  на векторное произведение векторов
на векторное произведение векторов 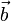 и
и 
![\left[ \vec{a}, \vec{b}, \vec{c}\right] = \left[\vec{a}, \left[\vec{b}, \vec{c}\right]\right].](/pictures/wiki/files/98/b4a0f2d97f92bdbf8128b5c059f22670.png)
В литературе этот тип произведения трёх векторов называется как тройным[1] (по числу векторов), так и двойным[2] (по числу операций умножения).
Свойства
Формула Лагранжа
Для тройного векторного произведения справедлива формула Лагранжа,
![\left[ \vec{a}, \vec{b}, \vec{c} \right] = \vec{b} \left( \vec{a} \cdot \vec{c} \right) - \vec{c} \left( \vec{a} \cdot \vec{b} \right),](/pictures/wiki/files/49/1c5e6e3f9a366e3bddb24a5f5e454705.png)
которую можно запомнить по мнемоническому правилу «бац минус цаб».
Тождество Якоби
Для тройного векторного произведения выполняется тождество Якоби
![\left[ \vec{a}, \vec{b}, \vec{c} \right]+\left[ \vec{b}, \vec{c}, \vec{a} \right]+\left[ \vec{c}, \vec{a}, \vec{b} \right] = 0,](/pictures/wiki/files/52/4ca42dc4ee2810c9d98baf7332ebc7df.png)
которое доказывается раскрытием скобок по формуле Лагранжа

Примечания
- ↑ См., например, Weisstein, Eric W. Vector Triple Product на сайте Wolfram MathWorld.(англ.).
- ↑ См., например, М. Я. Выгодский, Справочник по высшей математике, М., 1977, стр. 156.
См. также
Wikimedia Foundation.
2010.
Полезное
Смотреть что такое "Векторно-векторное произведение векторов" в других словарях:
Векторное произведение векторов — Содержание 1 Правые и левые тройки векторов 2 Определение 3 Свойства … Википедия
Векторное произведение — в трёхмерном пространстве. Векторное произведение это псевдовектор, перпендикулярный плоскости, построенной по двум … Википедия
Векторное умножение — Содержание 1 Правые и левые тройки векторов 2 Определение 3 Свойства … Википедия
Оператор набла — (оператор Гамильтона) векторный дифференциальный оператор, обозначаемый символом (набла) (в Юникоде U+2207, ∇). Для трёхмерного евклидова пространства в прямоугольных декартовых координатах[1] оператор набла определяется следующим образом … Википедия
Момент силы — Размерность L2MT−2 Единицы измерения СИ Ньютон метр … Википедия
Вращательный момент — Момент силы (синонимы: крутящий момент; вращательный момент; вращающий момент) физическая величина, характеризующая вращательное действие силы на твёрдое тело. Момент силы приложенный к гаечному ключу Отношение между векторами силы, момента силы … Википедия
Вращающий момент — Момент силы (синонимы: крутящий момент; вращательный момент; вращающий момент) физическая величина, характеризующая вращательное действие силы на твёрдое тело. Момент силы приложенный к гаечному ключу Отношение между векторами силы, момента силы … Википедия
Крутящий момент — Момент силы (синонимы: крутящий момент; вращательный момент; вращающий момент) физическая величина, характеризующая вращательное действие силы на твёрдое тело. Момент силы приложенный к гаечному ключу Отношение между векторами силы, момента силы … Википедия
Механический момент — Момент силы (синонимы: крутящий момент; вращательный момент; вращающий момент) физическая величина, характеризующая вращательное действие силы на твёрдое тело. Момент силы приложенный к гаечному ключу Отношение между векторами силы, момента силы … Википедия
Момент сил — Момент силы (синонимы: крутящий момент; вращательный момент; вращающий момент) физическая величина, характеризующая вращательное действие силы на твёрдое тело. Момент силы приложенный к гаечному ключу Отношение между векторами силы, момента силы … Википедия
![\left[ \vec{a}, \vec{b}, \vec{c} \right]](/pictures/wiki/files/48/0e6a64ecd01d00a9fa21e04ac4c4f468.png) векторов
векторов 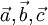 — векторное произведение вектора
— векторное произведение вектора  на векторное произведение векторов
на векторное произведение векторов 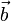 и
и 

![\left[ \vec{a}, \vec{b}, \vec{c}\right] = \left[\vec{a}, \left[\vec{b}, \vec{c}\right]\right].](/pictures/wiki/files/98/b4a0f2d97f92bdbf8128b5c059f22670.png)
![\left[ \vec{a}, \vec{b}, \vec{c} \right] = \vec{b} \left( \vec{a} \cdot \vec{c} \right) - \vec{c} \left( \vec{a} \cdot \vec{b} \right),](/pictures/wiki/files/49/1c5e6e3f9a366e3bddb24a5f5e454705.png)
 так, чтобы
так, чтобы


![\left[ \vec{b}, \vec{c} \right] = \left( 0, 0, -\beta_2\gamma_1 \right),](/pictures/wiki/files/48/0482b01cfe0ff761fb3f782decc72608.png)
![\left[ \vec{a}, \left[ \vec{b}, \vec{c} \right] \right] = \left( - \alpha_2\beta_2\gamma_1, \alpha_1\beta_2\gamma_1, 0 \right)](/pictures/wiki/files/99/c119e2d054a3c8399e48922542f47fdf.png)

![\left[ \vec{a}, \left[ \vec{b}, \vec{c} \right] \right] = \vec{b} \left( \vec{a} \cdot \vec{c} \right) - \vec{c} \left( \vec{a} \cdot \vec{b} \right).](/pictures/wiki/files/97/a7a6058584fac95a8f9b54d2072a7ffb.png)
![\left[ \vec{a}, \vec{b}, \vec{c} \right]+\left[ \vec{b}, \vec{c}, \vec{a} \right]+\left[ \vec{c}, \vec{a}, \vec{b} \right] = 0,](/pictures/wiki/files/52/4ca42dc4ee2810c9d98baf7332ebc7df.png)
