Варианта

Последовательность — функция 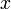$x\,\!$ одного натурального переменного, обладающая следующим свойством:

каково бы ни было принадлежащее области определения функции 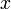$x\,\!$ натуральное число 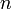$n\,\!$, любое удовлетворяющее условию 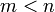$m<n\,\!$ натуральное число 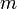$m\,\!$ также принадлежит области определения функции $x\,\!$.

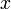Областью значений функции 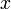$x\,\!$ может при этом быть произвольное множество X. Желая уточнить характер этой области, нередко говорят о «последовательности элементов множества X».

Значение 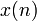$x(n)\,\!$ обычно называют членом последовательности 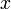$x\,\!$, имеющим номер $n\,\!$.

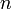Упорядоченные наборы 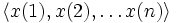$\langle x(1),\,\!x(2),\ldots x(n)\rangle$ первых 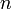$n\,\!$ членов последовательности (рассматриваемые в предположении о существовании члена 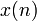$x(n)\,\!$) называют начальными отрезками последовательности.

Символика

При записи членов последовательностей номер обычно пишут не в скобках после символа функции, а в качестве нижнего индекса при этом символе. Например, вместо записи x(n) для n-го члена последовательности x применяют запись x_n.

Чаще всего рассматриваются последовательности, областью определения которых является весь натуральный ряд. С целью указать на такой характер области определения функции x используют обозначение 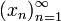$(x_n)_{n=1}^{\infty}$. Аналогично, для последовательностей, областью определения которых является отрезок натурального ряда вида

$I_N=\{n\in\mathbb N\mid n\leqslant N\}$,

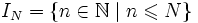используют обозначение $(x_n)_{n=1}^N$.

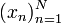Примеры

• Функция 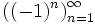$\left((-1)^n\right)_{n=1}^{\infty}$ является бесконечной последовательностью целых чисел. Начальные отрезки этой последовательности имеют вид $\langle -1, 1, -1, 1, -1,\ldots\rangle$.
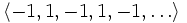• Функция 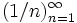$(1/n)_{n=1}^{\infty}$ является бесконечной последовательностью рациональных чисел. Начальные отрезки этой последовательности имеют вид $\langle 1, 1/2, 1/3, 1/4, 1/5,\ldots\rangle$.
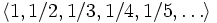• Функция, сопоставляющая каждому натуральному числу 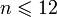$n\leqslant 12$ одно из слов «январь», «февраль», «март», «апрель», «май», «июнь», «июль», «август», «сентябрь», «октябрь», «ноябрь», «декабрь» (в порядке их следования здесь) представляет собой последовательность вида 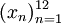$(x_n)_{n=1}^{12}$. В частности, пятым членом x₅ этой последовательности является слово «май».

Типы последовательностей

• Бесконечно малая — последовательность, предел которой равен 0.
• Бесконечно большая — последовательность, предел которой равен бесконечности.
• Стационарная — последовательность, все члены которой, начиная с некоторого, равны.

Вариации и обобщения

• Циклическая последовательность — отображение циклической группы $\Z_n\to X$.

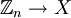См. также

• Энциклопедия целочисленных последовательностей
• Предел последовательности