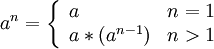Быстрое возведение в степень
- Быстрое возведение в степень
-
Алгоритм быстрого возведения в степень — алгоритм, предназначенный для возведения числа x в натуральную степень n за меньшее число умножений, чем это требуется в определении.
Алгоритм не всегда оптимален. Например, при n=15 требуется 6 умножений, хотя на самом деле возведение в 15-ую степень можно выполнить за 5 умножений.
Теоретические основы алгоритма
Пусть 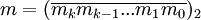 — двоичное представление степени n. Тогда
— двоичное представление степени n. Тогда 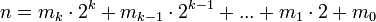 , где
, где 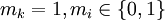 и
и 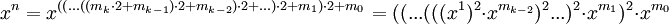 .
.
Таким образом, алгоритм быстрого возведения в степень сводится к мультипликативному аналогу схемы Горнера.
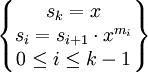
Программная реализация
Используется представление числа xm:
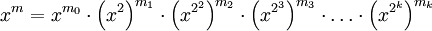 .
.
int power(int t, int k) {
// возведение t в степень k
int res = 1;
while (k) {
if (k & 1) res *= t;
t *= t;
k >>= 1;
}
return res;
}
function power(t,k:integer):integer;
var
res:integer;
Begin
res := 1;
while (k > 0) do
begin
if (k mod 2 = 1) then {или напишите "if (k and 1 = 1)" для бОльшей скорости выполнения}
res := res * t;
t := t * t;
k := k div 2; {или напишите "k := k shr 1;" для бОльшей скорости выполнения}
end;
power := res;
End;
Оценка сложности
Чтобы узнать, сколько умножений потребуется для возведения числа x в степень n алгоритмом быстрого возведения в степень, нужно произвести вычисления по следующей формуле: k = H + 2(E − 1), где H — количество нулей, а E — количество единиц в двоичной записи числа n.
Так, для возведения числа в сотую степень этим алгоритмом потребуется всего лишь 8 умножений.
Таким образом количество умножений равно O(lnn).
Обобщение
Пусть пара (S, *) — полугруппа, то есть S — произвольное множество, на котором задана бинарная операция * такая, что:
- Для любых элементов a и b из S справедливо: (a * b) так же из S. (замкнутость)
- Для любых элементов a, b и c из S справедливо: ((a * b) * c) = (a * (b * c)). (ассоциативность)
Мы можем назвать операцию * умножением и определить операцию возведения в натуральную степень:
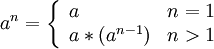
Для вычисления значений an можно использовать алгоритм быстрого возведения в степень.
Литература
- Валицкас А. И. Конспект лекций по дисциплине: Элементы абстрактной и компьютерной алгебры. //Тобольск, ТГПИ им. Д. И. Менделеева, 2004.
Wikimedia Foundation.
2010.
Полезное
Смотреть что такое "Быстрое возведение в степень" в других словарях:
Алгоритм быстрого возведения в степень — Алгоритм быстрого возведения в степень алгоритм, предназначенный для возведения числа x в натуральную степень n за меньшее число умножений, чем это требуется в определении степени. Алгоритм не всегда оптимален: например, быстрое возведение… … Википедия
Список алгоритмов — Эта страница информационный список. Основная статья: Алгоритм Ниже приводится список алгоритмов, группированный по категориям. Более детальные сведения приводятся в списке структур данных и … Википедия
Программируемые алгоритмы — Служебный список статей, созданный для координации работ по развитию темы. Данное предупреждение не устанавл … Википедия
Логарифм — График двоичного логарифма Логарифм числа … Википедия
Толстой, граф Лев Николаевич — знаменитый писатель, достигший еще небывалой в истории литературы XIX в. славы. В его лице могущественно соединились великий художник с великим моралистом. Личная жизнь Т., его стойкость, неутомимость, отзывчивость, одушевление в отстаивании… … Большая биографическая энциклопедия
Алгебра — Общие сведения Алгебра один из больших разделов математики (См. Математика), принадлежащий наряду с арифметикой (См. Арифметика) и геометрией (См. Геометрия) к числу старейших ветвей этой науки. Задачи, а также методы А.,… … Большая советская энциклопедия
Александр II (часть 2, XIII-XIX) — XIII. Дела внутренние (1866—1871). 4 го апреля 1866 года, в четвертом часу дня, Император Александр, после обычной прогулки в Летнем саду, садился в коляску, когда неизвестный человек выстрелил в него из пистолета. В эту минуту, стоявший в… … Большая биографическая энциклопедия
СССР. Технические науки — Авиационная наука и техника В дореволюционной России был построен ряд самолётов оригинальной конструкции. Свои самолёты создали (1909 1914) Я. М. Гаккель, Д. П. Григорович, В. А. Слесарев и др. Был построен 4 моторный самолёт… … Большая советская энциклопедия
Китай государство в Азии — Содержание: География. История общая. История сношений К. с Европой. Язык и литература. Китайская музыка. Великая империя восточной и центральной Азии известна среди своих обитателей под названиями, ничего общего с европейскими (Китай, China,… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Китай, государство в Азии — Содержание: География. История общая. История сношений К. с Европой. Язык и литература. Китайская музыка. Великая империя восточной и центральной Азии известна среди своих обитателей под названиями, ничего общего с европейскими (Китай, China,… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
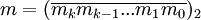 — двоичное представление степени n. Тогда
— двоичное представление степени n. Тогда 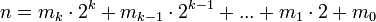 , где
, где 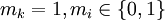 и
и 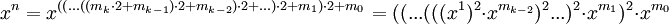 .
.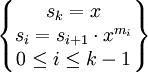
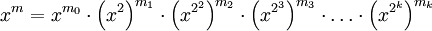 .
.