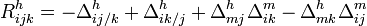Биметрическая теория

Биметрическая теория относится к классу модифицированных теорий гравитации, в которой два метрических тензора используются вместо одного. Часто вторая метрика вводится при высоких энергиях, в смысле, что скорость света может быть энергетической зависимости.

В общей теории относительности можно предположить, что расстояние между двумя точками в пространственно приведен в метрического тензора. Эйнштейна поля затем используются для расчета форме метрики основанных на распределении энергии.

Розен (1940) предложил в каждой точке пространства-времени евклидова метрического тензора g_ij в дополнение к римановы метрического тензора g_ij. Таким образом, в каждой точке пространства-времени есть два показателя:

ds² = g_ijdxⁱdx^j

dσ² = γ_ijdxⁱdx^j

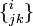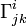Первый метрический тензор g_ij описание геометрии пространства-времени и, таким образом, гравитационное поле. Второй метрического тензора γ_ij относится к плоским пространства-времени и описывает инерционным силам. В Кристоффеля символы формируются из γ_ij и γ_ij обозначаются на $\{^{i}_{jk}\}$ и $\Gamma^{i}_{jk}$ соответственно. Количества Δ определены таким образом, чтобы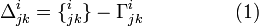

$\Delta^{i}_{jk}=\{^{i}_{jk}\}-\Gamma^{i}_{jk}~~~~~~~~~~~~~~(1)$

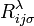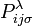Теперь возникают два вида ковариантного дифференцирования: g дифференцирование, основанная на g_ij (обозначается запятой (;)), 3 - дифференциация на основе γ_ij (обозначается объявлений), обычные частные производные обозначаются запятой (,). $R^{\lambda}_{ij \sigma}$ и $P^{\lambda}_{ij \sigma}$ быть тензоров кривизны рассчитывается из g_ij и γ_ij соответственно. На основе вышеизложенного подхода, как γ_ij является плоской пространственно-временной метрики, тензор кривизны 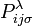$P^{\lambda}_{ij \sigma}$ равен нулю.

Из (1) следует, что хотя (:) и Γ не есть тензоры, но Δ является тензором, имеющих такую же форму, как (:) за исключением того, что обычные частные производные заменяется 3-ковариантной производной. Простой расч`т

$R^{h}_{ijk}=-\Delta^{h}_{ij/k}+\Delta^{h}_{ik/j}+\Delta^{h}_{mj}\Delta^{m}_{ik}-\Delta^{h}_{mk}\Delta^{m}_{ij}$

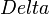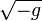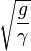Каждое слово по правой стороне (1.6.4) является тензором. Видно, что из общей теории относительности (ОТО), можно перейти на новые разработки, просто заменив (:) на $\ Delta$ очередные дифференциации 3-ковариантного дифференцирования, $\sqrt {-g}$ by $\sqrt{\frac{g}{\gamma}}$ в интеграции d⁴x by 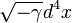$\sqrt {-\gamma}d^{4}x$, где g = det(g_ij), 3 = det(γ_ij) и d⁴x = dx¹dx²dx³dx⁴. Необходимо отметить, что, как только представил γ_ij в теории, то большое число новых тензоров и скаляров в одно распоряжение. Один можно настроить поля, кроме Эйнштейна поля. Вполне возможно, что некоторые из них будут более удовлетворительными для описания природы.

В геодезических уравнения в bimetric относительности (BR) принимает форму

$\frac{d^2x}{ds^2}+\Gamma^{i}_{jk}\frac{dx^{j}}{ds}\frac{dx^{k}}{ds}+\Delta^{i}_{jk}\frac{dx^{j}}{ds}\frac{dx^{k}}{ds}=0~~~~~~~~~~~~~~(2)$

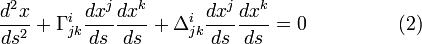
Это видно из уравнения (1) и (2), что 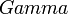$\ Gamma$ можно рассматривать как описывающие инерциальное области, поскольку он исчезает с помощью соответствующего преобразования координат.

Количество 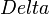$\ Delta$ время тензорными является независимой от каких-либо системе координат, и, следовательно, может рассматриваться в качестве постоянных, описывающих гравитационное поле.

Розен (1973) были найдены BR удовлетворяющих ковариантность и принцип эквивалентности. В 1966 г. Розен показала, что введение метрического пространства в рамках общей теории относительности, не только позволяет получить плотность энергии импульса тензор гравитационного поля, но также позволяет получить этот тензор из вариационного принципа. В поле БР, полученных из вариационного принципа

$K^{i}_{j}= N^{i}_{j}-\frac{1}{2}\delta^{i}_{j}N = -8 \pi \kappa T^{i}_{j}~~~~~~~~~~~~~~(3)$

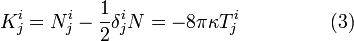
где

$N^{i}_{j}=\frac{1}{2}\gamma^{\alpha \beta}(g^{hi} g_{hj /\alpha})/ \beta$

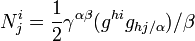
или

$N^{i}_{j}= \gamma^{\alpha \beta}\left\{(g^{hi}g_{hj, \alpha}),\beta - (g^{hi}g_{mj}\Gamma^{m}_{h\alpha}),\beta\right\} -\gamma^{\alpha \beta}(\Gamma^{i}_{j\alpha}),\beta+ \Gamma^{i}_{\lambda \beta}[g^{h\lambda}g_{hj},\alpha - g^{h\lambda}g_{mj}\Gamma^{m}_{h\alpha} -\Gamma^{\lambda}_{j\alpha}]-\Gamma^{\lambda}_{j\beta}[g^{hi}g_{h\lambda},\alpha - g^{hi}g_{m\lambda}\Gamma^{m}_{h\alpha} -\Gamma^{i}_{\lambda\alpha}]$

$+ \Gamma^{\lambda}_{\alpha \beta}[g^{hi}g_{hj},\lambda - g^{hi}g_{mj}\Gamma^{m}_{h\lambda} -\Gamma^{i}_{j\lambda}]$

$N= g^{ij}N_{ij}, \kappa=\sqrt{\frac{g}{\gamma}},$

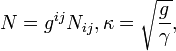
и T⁽I)₍J) = энергии импульса. \ \ В вариационного принципа приводит также к связи

$T^{i}_{j;i}=0.$

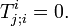
Поэтому из (3)

$K^{i}_{j;i}=0,$

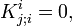
, которая подразумевает, что в БР испытание частицы в гравитационном поле движется по геодезической в связи с g_ij. Оказалось, что теория и BR GR различаться в следующих случаях:

• Распространения электромагнитных волн
• Внешнем поле высокой плотности звезд
• Поведение интенсивные гравитационных волн через сильное статическое гравитационное поле

Примечания

Ссылки

Теории гравитации

Классическая теория тяготения Ньютона Общая теория относительности Квантовая гравитация Альтернативные Классическая механика Гравитационная постоянная Математическая формулировка общей теории относительности Принцип эквивалентности сил гравитации и инерции Гравитомагнетизм Гравитация с массивным гравитоном Телепараллелизм Геометродинамика (англ.) Теория Нордстрёма Петлевая квантовая гравитация Теория струн М-теория Теория Калуцы — Клейна Супергравитация Теория Бранса — Дикке Исключительно простая теория всего Полуклассическая гравитация (англ.) Теория гравитации Лесажа Биметрические теории Несимметричные теории гравитации Скаляр-тензор-векторная гравитация (англ.) Теория гравитации Уайтхеда (англ.) Модифицированная ньютоновская динамика (англ.) Составная гравитация (англ.)