Теорема Вариньона (геометрия)

У этого термина существуют и другие значения, см. Теорема Вариньона.

Иллюстрация к теореме Вариньона. Красный четырёхугольник — параллелограмм

Теоре́ма Вариньо́на — геометрический факт, доказанный Пьером Вариньоном:

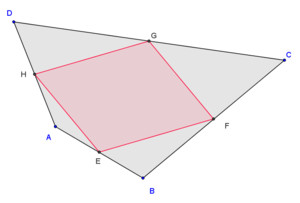
Четырёхугольник, вершины которого совпадают с серединами сторон произвольного четырёхугольника, является параллелограммом, стороны которого параллельны диагоналям исходного четырёхугольника.

или сокращённо

Середины сторон произвольного четырёхугольника — вершины параллелограмма

Параллелограмм, образованный серединами сторон, иногда называется вариньоновским или вариньоновым.

Центр параллелограмма Вариньона лежит на середине отрезка, соединяющего середины сторон исходного четырёхугольника (в этой же точке пересекаются отрезки, соединяющие середины противоположных сторон — диагонали вариньоновского параллелограмма).

Площадь параллелограмма Вариньона равна половине площади исходного четырёхугольника.

Следствие из теоремы: для прямоугольника и равнобедренной трапеции параллелограммом Вариньона является ромб, а для ромба — прямоугольник.

Доказательство  

Проведём диагональ AC. Отрезки EF и GH будут средними линиями треугольников $\triangle ABC$ и $\triangle ADC$. По теореме о средней линии, отрезки будут параллельны диагонали, а, значит, и друг другу. Повторив аналогичные рассуждения для диагонали BD, получаем, что противоположные стороны четырёхугольника EFGH параллельны, и, по определению, это — параллелограмм.

Доказательство, что площадь параллелограмма равна половине площади исходного четырехугольника: Пусть диагональ $AC$ проходит внутри четырёхугольника. Тогда площадь треугольника $ABC$ равна $\frac{AC\cdot h_b}2$, где $h_b$ --- высота треугольника $ABC$, проведённая из вершины $B$. Аналогично, площадь треугольника $ADC$ равна $\frac{AC\cdot h_d}2$. Тогда площадь всего четырёхугольника равна $\frac{AC(h_b+h_d)}2$. Но $\frac{(h_b+h_d)}2=\frac{h_b}2+\frac{h_d}2$ — это сумма расстояний до прямой $AC$ от точек $E$ и $H$, то есть в точности высота параллелограмма $EHGF$. А поскольку сторона $GH$ параллелограмма вдвое меньше $AC$, то и площадь параллелограмма равна половине площади $ABCD$, Q. E. D.