- Линейная вектор-функция
-
Линейная вектор-функция
Линейная вектор-функция, функция f(x) векторного переменного х, обладающая следующими свойствами:
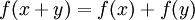
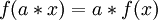 (a - число).
(a - число).
Л. в.-ф. в n-мерном пространстве вполне определяется значениями, принимаемыми ею для n линейно независимых векторов. Скалярную (принимающую числовые значения) Л. в.-ф. называют также линейным функционалом; в n-mepном пространстве она выражается линейной формой,
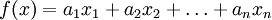 от координат
от координат 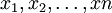 вектора х. Примером скалярной Л. в.-ф. является скалярное произведение вектора х и некоторого постоянного вектора а:
вектора х. Примером скалярной Л. в.-ф. является скалярное произведение вектора х и некоторого постоянного вектора а: 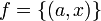 , в пространстве, в котором определено скалярное произведение, всякая скалярная Л. в.-ф. имеет такой вид. Векторная (принимающая векторные значения) Л. в.-ф. определяет линейное или аффинное преобразование пространства и называется также линейным оператором, или аффинором. Векторная Л. в.-ф. y = f(x) в n-мерном пространстве выражается в координатах формулами:
, в пространстве, в котором определено скалярное произведение, всякая скалярная Л. в.-ф. имеет такой вид. Векторная (принимающая векторные значения) Л. в.-ф. определяет линейное или аффинное преобразование пространства и называется также линейным оператором, или аффинором. Векторная Л. в.-ф. y = f(x) в n-мерном пространстве выражается в координатах формулами: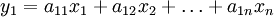 ,
,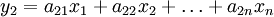 ,
,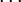
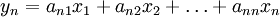 .
.Здесь числа aij
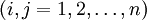 составляют матрицу векторной Л. в.-ф. Если определить сумму векторных Л. в.-ф.
составляют матрицу векторной Л. в.-ф. Если определить сумму векторных Л. в.-ф. 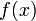 и
и 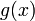 как Л. в.-ф.
как Л. в.-ф. 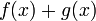 , а произведение тех же функций, как Л. в.-ф.
, а произведение тех же функций, как Л. в.-ф. 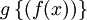 , то сумме и произведению векторных Л. в.-ф. будут соответствовать сумма и произведение соответствующих матриц. Примером векторной Л. в.-ф. является Л. в.-ф. вида:
, то сумме и произведению векторных Л. в.-ф. будут соответствовать сумма и произведение соответствующих матриц. Примером векторной Л. в.-ф. является Л. в.-ф. вида: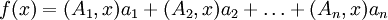 ,
,где
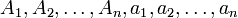 - постоянные векторы; в n-мерном пространстве, в котором определено скалярное произведение, всякая векторная Л. в.-ф. может быть представлена в таком виде.
- постоянные векторы; в n-мерном пространстве, в котором определено скалярное произведение, всякая векторная Л. в.-ф. может быть представлена в таком виде.Функцию нескольких векторных переменных, являющуюся Л. в.-ф. относительно каждого своего аргумента, называют полилинейной (билинейной, трилинейной и т. д.) вектор-функцией. Скалярное и векторное произведения двух переменных векторов могут служить примерами, соответственно скалярной и векторной билинейных вектор-функций. Полилинейные вектор-функции приводят к понятию тензора. О Л. в.-ф. (линейных функционалах и операторах) в бесконечномерном пространстве см. Функциональный анализ.
Wikimedia Foundation. 2010.
