Квантовая индуктивность (графен)

Квантовая индуктивность (графен)

Связать^?

Квантовая индуктивность (графен) (Quantum Inductance (Graphene)) – новая физическая величина, которая может быть получена из подхода Лурия (1988) ^[1], разработанного для квантовой емкости при описании двумерного электронного газа на поверхности кремния и AsGa-гетероструктур. Эта индуктивность определяется через стандартную плотность состояний в твердом теле. Квантовая индуктивность может быть использована при исследовании КЭХ (целочисленного и дробного), как новый подход, который использует концепцию квантового LC контура.

Теория

В общем случае двумерная плотность состояний в твердом теле может быть представлена в следующем виде:

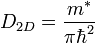$D_{2D} = \frac{m^*}{\pi \hbar^2} \$, (1)

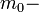где $m^* = \xi m_0 - \$ эффективная масса свободных носителей тока в твердом теле, $m_0 - \$ масса электрона, и 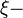$\xi - \$ безразмерный параметр, который учитывает зонную структуру твердого тела. Таким образом, квантовая индуктивность может быть определена следующим образом:

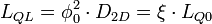$L_{QL} = \phi_0^2\cdot D_{2D} = \xi \cdot L_{Q0}$, (2)

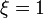где $L_{Q0} = 8\pi \beta \cdot L_{QY} \$ - идеальное значение квантовой индуктивности при $\xi = 1 \$, и другая идеальная квантовая индуктивность:

$L_{QY} = \frac{\mu_0}{\lambda_0} = 517921,27 H/m^2 \$, (3)

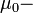где $\mu_0 - \$ магнитная проницаемость, 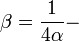$\beta = \frac{1}{4\alpha} - \$ магнитная “постоянная тонкой структуры”^[2](стр.62), 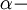$\alpha - \$ постоянная тонкой структуры and 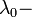$\lambda_0 - \$ комптоновская длина волны электрона, впервые предложенная Якимахой (1994) ^[3] при спектроскопических исследованиях МДП-транзисторов при комнатных температурах.

Квантовый эффект Холла

Поскольку определенная выше квантовая индуктивность имеет размерность на единицу площади, поэтому ее абсолютное значение в режиме КЭХ будет:

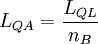$L_{QA} = \frac{L_{QL}}{n_B} \$ (4)

где концентрация носителей тока равна:

$n_B = \frac{eB}{h} \$.

Здесь $h - \$ постоянная Планка. Аналогичным образом можно ввести абсолютное значение для квантовой емкости в КЭХ:

$C_{QA} = \frac{C_{QL}}{n_B} \$, (5)

где

$C_{QL} = e^2\cdot D_{2D} = \xi \cdot C_{Q0}$, (6)

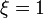определение квантовой емкости по Лурию^[1], $C_{Q0} = 8\pi \alpha \cdot C_{QY} \$ - ‘’идеальное значение’’ квантовой емкости при $\xi = 1 \$, а другая идеальная квантовая емкость равна:

$C_{QY} = \frac{\epsilon_0}{\lambda_0} = 3,6492417 F/m^2 \$, (7)

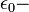где $\epsilon_0 - \$ диэлектрическая постоянная, впервые определенная Якимахой (1994) )^[3] при спектроскопических исследованиях МДП-транзисторов при комнатных температурах.

Стандартное определение волнового импеданса для КЭХ LC-контура может быть представлено в виде:

$\rho_Q = \sqrt{\frac{L_{QA}}{C_{QA}}} = \sqrt{\frac{\phi_0^2}{e^2}} = \frac{h}{e^2} = R_H \$, (6)

где $R_H = \frac{h}{e^2} = 25.812813 k\Omega \$ постоянная Клитцинга для сопротивления.

Стандартное определение резонансной частоты для КЭХ LC-контура может быть представлено в виде:

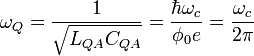$\omega_Q = \frac{1}{\sqrt{L_{QA}C_{QA}}} = \frac{\hbar \omega_c}{\phi_0e} = \frac{\omega_c}{2\pi}$, (7)

где $\omega_c = \frac{eB}{m^*} - \$ стандартная циклотронная частота в магнитном поле B.

Эксперименты

Квантовый эффект Холла

Первые попытки исследования реактивных параметров LC-контура КЭХ были предприняты Кэйджем и Джеффри (1996) ^[4]. Данные исследования проводились в рамках программы измерений стандарта сопротивления на переменном токе. Представленная модель LC-контура базировалась на классическом подходе, и квантовые значения для емкости и индуктивности не вводились.

Кремниевые МДП-транзисторы

Первый квантовый резонансный LC-контур был обнаружен в 1994 году ^[3] при спектроскопических исследованиях МДП-транзисторов в диапазоне частот 100Гц – 20кГц. Полученное значение для циклической резонансной частоты (5088 рад/с), позволило сделать оценки значений квантовых реактивных параметров. При этом квантовая емкость определялась выражением:

$C_{0X} = \frac{\epsilon_0S_{MOS}}{\lambda_0}\cdot \frac{\lambda_{CX}}{\lambda_0} \$

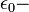где $\epsilon_0 - \$ диэлектрическая постоянная, $S_{MOS} - \$ площадь поверхности МДП-транзистора и $\lambda_{CX} - \$ толщина плоской квантовой емкости. Квантовая индуктивность определялась выражением:

$L_{0X} = \frac{\mu_0S_{MOS}}{\lambda_0}\cdot \frac{\lambda_{LX}}{\lambda_0} \$,

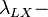где $\lambda_{LX} - \$ толщина плоской квантовой индуктивности. В результате исследований было экспериментально доказано, что толщины квантовой емкости и индуктивности равны комптоновской длине волны электрона:

$\lambda_{CX} = \lambda_{LX} = \lambda_0 \$.

Резонансное туннелирование

См. также

• Квантовый зарядовый осциллятор
• Квантовая емкость (графен)

Примечания

1. ↑ ^{1 2} Serge Luryi (1988). "Quantum capacitance device". Appl. Phys. Lett. 52(6). Pdf
2. ↑ Yakymakha O.L.(1989). High Temperature Quantum Galvanomagnetic Effects in the Two- Dimensional Inversion Layers of MOSFET's (In Russian). Kyiv: Vyscha Shkola. p.91. ISBN 5-11-002309-3. djvu
3. ↑ ^{1 2 3} Yakymakha O.L., Kalnibolotskij Y.M. (1994). "Very-low-frequency resonance of MOSFET amplifier parameters". Solid- State Electronics 37(10), 1739-1751 pdf
4. ↑ M. E. Cage and A. Jeffery (1996).. “Intrinsic Capacitances and Inductances of Quantum Hall Effect Devices”. ‘’J. Res. Natl. Inst. Stand. Technol.’’ 101(6), 733