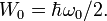Квантовый зарядовый осциллятор

Квантовый зарядовый осциллятор (Quantum Charge Oscillator) — аналитическое продолжение классического LC ? осциллятора (колебательного контура) на область квантовой механики. Из классической электродонамики известно дифференциальное уравнение для реактивного колебательного контура в виде:

$L\frac{d^2q}{dt^2} + R\frac{dq}{dt} + \frac{q}{C} = 0$

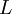где $L \$ — индуктивность контура, $R \$- активное сопротивление системы (за счет соединительных проводников) и $C \$- емкость контура.

По своей математической форме и по физическому содержанию это классическое дифференциальное уравнение эквивалентное дифференциальному уравнению свободных затухающих колебаний шара, подвешенного на пружине:

$m\frac{d^2x}{dt^2} + r\frac{dx}{dt} + kx = 0$

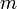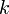где $m \$- масса шарика, $r \$ механическое сопротивление колебаниям маятника и $k \$- коэффициент упругости.

Таким образом, в классической физике мы имеем взаимное соответствие между механичными и электродинамическими физическими величинами:

$L \leftrightarrow m$ (индуктивность <--> масса)

$C \leftrightarrow 1/k$ (емкость <--> 1/упругость)

$x \leftrightarrow q$ (смещения <--> заряд).

Необходимо отметить, что все это было давно известно, и не только в 60-х годах прошлого века, а и в 20-х. Поэтому может возникнуть тривиальный вопрос, почему классический механический осциллятор был распространен на область квантовой механики, а электродинамический осциллятор — нет? Очевидно, что ответ на данный вопрос следует искать не в технических трудностях перехода в область квантовой механики (поскольку с точки зрения математики такой переход достаточно тривиален!), а в отсутствии «социального заказа» на данный переход. Но с открытием Якимахой в средине 90-х годов прошлого века «плоского атома» в однородном электрическом поле МДП- транзистора, такой «социальный заказ» появился. Ниже представлены результаты аналитического перехода от классической области в квантовую.

Квантовые операторы электромагнитных величин

Оператор импульса в зарядовом пространстве можно подать в следующем виде:

$\hat p_L = -i\hbar \frac{d}{dq}, \hat p_L^* = i\hbar \frac{d}{dq}$

где $\hbar-$ приведенная постоянная Планка, а $\hat p_L^*$- комплексно- сопряженный оператор импульса. Оператор Гамильтона в зарядовом пространстве можно представить в виде:

$\hat H_L = -\frac{\hbar^2}{2L}\frac{d^2}{dq^2} + \frac{L\omega_0^2}{2}\hat q^2$

где $\hat q^* -$ комплексно- сопряженный оператор заряда, а

$\omega_0 = \sqrt{\frac{1}{LC} - \frac{R^2}{4L^2}} -$ резонансная частота колебательного контура. Единствыенное отличие зарядового пространства от традиционного 3Д- пространства в том, что он одномерный. Правда в нем негативные координаты необходимо принимать вполне всерйоз, поскольку они связаны с зарядами!

Уравнение Шредингера для электромагнитного осциллятора

Используя операторы зарядового пространства, уравнение Шредингера для электромагнитного осциллятора можно записать в виде:

$-\frac{\hbar^2}{2L}\frac{d^2 \Psi}{dq^2} + \frac{L\omega_0^2}{2}q^2\Psi = W\Psi$

Для решения этого уравнения необходимо ввести безразмерные переменные для зарядов и энергии:

$\xi = \sqrt{\frac{a}{b} = \frac{a}{b}}$

$\lambda = \frac{2W}{\hbar\omega_0}$

где $q_0 = \sqrt{\frac{\hbar}{L\omega_0}}$- масштабный заряд.

Тогда уравнение Шредингера в безразмерных переменных принимает форму уравнения Чебышева- Эрмита:

$(\frac{d^2}{d\xi^2} + \lambda - \xi^2)\Psi = 0$

Собственные значения гамильтониана здесь будут:

$W_n = \hbar \omega_0(n + 1/2). \$

где при n = 0 имеем «нульовые колебания»:

$W_0 = \hbar \omega_0/2. \$

В общем случае масштабный заряд можно записать в виде:

$q_0 = \sqrt{\frac{\hbar}{L\omega_0}} = \frac{q}{\sqrt{4\pi \alpha }}$

где $\alpha \$- постоянная тонкой структуры. Очевидно, что масштабный заряд существенно отличается од заряда электрона. Более того, его квантование будет:

$q_{0n} = q_0\sqrt{2n +1}, n = 0,1,2,... \$.

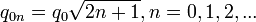Основные соотношения для реактивного квантового контура

Очевидно, что величины квантовых индуктивностей и емкостей взаимосвязаны. В квантовом случае так само, как и в классическом, мы имеем следующие соотношения для резонансной частоты и волнового сопротивления:

$\omega_q = \frac{1}{\sqrt{LC}} \$

$\rho_q = \sqrt{\frac{L}{C}}$

Эта система уравнений дает возможность нахождения реактивных параметров:

$C = \frac{1}{\omega_q \rho_q} \$

$L = \frac{\rho_q}{\omega_q} \$

Но волновое сопротивление в классической электродинамике равно величине:

$\rho_q = \sqrt{\frac{L}{C}} = \sqrt{\frac{\mu_0 \mu}{\epsilon_0 \epsilon }}$.

А в квантовом случае с учетом соотношений:

$\mu = \epsilon = 1 \$

мы будем иметь волновое сопротивление вакуума:

$\rho_q = \sqrt{\frac{\mu_0 }{\epsilon_0 }} = \rho_0.$.

На резонансную частоту LC ? контура также накладається умова:

$\omega_0 = \omega_q \$.

В общем случае полная энергия контура есть постоянная величина:

$W_t = \frac{Cq^2}{2} + \frac{LI^2}{2} = const.$

Приравнивая эту энергию нулевым колебаниям, находим максимальный ток в контуре:

$I_0^2 = \frac{\hbar \rho_0}{L^2}$

А в случае нулевого тока в контуре, получаем максимальный заряд на емкости:

$Q_0^2 = \frac{\hbar }{\rho_0 C^2}$

Между этими величинами справедливо соотношение:

$I_0Q_0 = \hbar \omega_0 \$.

См. также

• Гармонический осциллятор
• Квантовый осциллятор
• Квантовая индуктивность (графен)
• Квантовая емкость (графен)

Литература

• Яворский Б.М, Детлаф А. А., Милковская Л. Б. Курс физики. Т.2. Электричество и магнетизм, Изд. 3-е испр., М.:Высшая школа, 1966.-412 с.
• Кузьмичев В. Е. Законы и формулы физики.- Киев: Наук. думка, 1989.- 864 с.
• Yakymakha O.L., Kalnibolotskij Y.M., Solid- State Electronics, vol.37, No.10,1994.,pp.1739-1751 Pdf
• Yakymakha O.L., Kalnibolotskij Y.M., Solid- State Electronics, vol.38, No.3,1995.,pp.661-671 pdf
• Yakymakha O.L., High Temperature Quantum Galvanomagnetic Effects in the Two- Dimensional Inversion Layers of MOSFET’s, p.91. Vyscha Shkola, Kyiv (1989).