- Затухающие колебания
-
 Затухающие колебания пружинного маятника
Затухающие колебания пружинного маятникаЗатухающие колебания — колебания, энергия которых уменьшается с течением времени. Бесконечно длящийся процесс вида
 в природе невозможен. Свободные колебания любого осциллятора рано или поздно затухают и прекращаются. Поэтому на практике обычно имеют дело с затухающими колебаниями. Они характеризуются тем, что амплитуда колебаний A является убывающей функцией. Обычно затухание происходит под действием сил сопротивления среды, наиболее часто выражаемых линейной зависимостью от скорости колебаний
в природе невозможен. Свободные колебания любого осциллятора рано или поздно затухают и прекращаются. Поэтому на практике обычно имеют дело с затухающими колебаниями. Они характеризуются тем, что амплитуда колебаний A является убывающей функцией. Обычно затухание происходит под действием сил сопротивления среды, наиболее часто выражаемых линейной зависимостью от скорости колебаний  или её квадрата.
или её квадрата.В акустике: затухание — уменьшение уровня сигнала до полной неслышимости.
Содержание
Затухающие колебания пружинного маятника
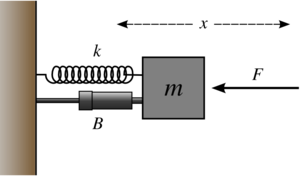 Модель пружинного маятника. B — механизм, обеспечивающий затухание. F — внешняя сила (в примере не присутствует).
Модель пружинного маятника. B — механизм, обеспечивающий затухание. F — внешняя сила (в примере не присутствует).
Пускай имеется система, состоящая из пружины (подчиняющейся закону Гука), один конец которой жёстко закреплён, а на другом находится тело массой m. Колебания совершаются в среде, где сила сопротивления пропорциональна скорости с коэффициентом c (см. вязкое трение).
Тогда второй закон Ньютона для рассматриваемой системы запишется так:

где
 — сила сопротивления,
— сила сопротивления,  — сила упругости
— сила упругости ,
,  , то есть
, то есть
или в дифференциальной форме

где k — коэффициент упругости в законе Гука, c — коэффициент сопротивления, устанавливающий соотношение между скоростью движения грузика и возникающей при этом силой сопротивления.
Для упрощения вводятся следующие обозначения:

Величину
 называют собственной частотой системы,
называют собственной частотой системы,  — коэффициентом затухания.
— коэффициентом затухания.Тогда дифференциальное уравнение принимает вид

Сделав замену
 , получают характеристическое уравнение
, получают характеристическое уравнение
Корни которого вычисляются по следующей формуле

Решения
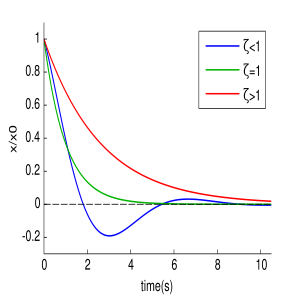
В зависимости от величины коэффициента затухания решение разделяется на три возможных варианта.
- Апериодичность
Если
 , то имеется два действительных корня, и решение дифференциального уравнения принимает вид:
, то имеется два действительных корня, и решение дифференциального уравнения принимает вид:
В этом случае колебания с самого начала экспоненциально затухают.
- Граница апериодичности
Если
 , два действительных корня совпадают
, два действительных корня совпадают  , и решением уравнения является:
, и решением уравнения является:
В данном случае может иметь место вре́менный рост, но потом — экспоненциальное затухание.
- Слабое затухание
Если
 , то решением характеристического уравнения являются два комплексно сопряжённых корня
, то решением характеристического уравнения являются два комплексно сопряжённых корня
Тогда решением исходного дифференциального уравнения является

Где
 — собственная частота затухающих колебаний.
— собственная частота затухающих колебаний.Константы
 и
и  в каждом из случаев определяются из начальных условий:
в каждом из случаев определяются из начальных условий: 
См. также
- Сейсмоосциллятор
- Декремент затухания
Литература
Лит.: Савельев И. В., Курс общей физики:Механика, 2001.
В этой статье не хватает ссылок на источники информации. Информация должна быть проверяема, иначе она может быть поставлена под сомнение и удалена.
Вы можете отредактировать эту статью, добавив ссылки на авторитетные источники.
Эта отметка установлена 13 мая 2011.Категория:- Теория колебаний
Wikimedia Foundation. 2010.