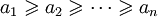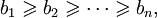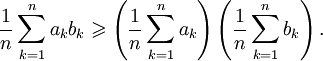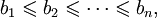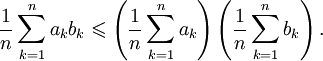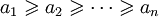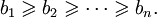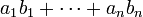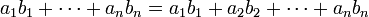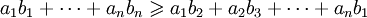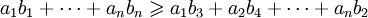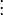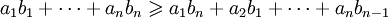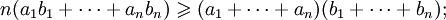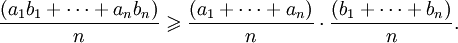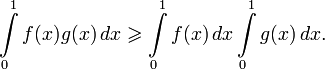- Неравенство Чебышёва для сумм
-
Неравенство Чебышёва для сумм
- В теории меры и теории вероятностей существует другое неравенство, носящее имя Чебышёва - см. Неравенство Чебышёва.
Неравенство Чебышева для сумм, носящее имя Пафнутия Львовича Чебышёва, утверждает, что если
и
то
Аналогично, если
и
то
Доказательство
Неравенство Чебышева для сумм легко выводится из перестановочного неравенства:
Предположим, что
и
В виду перестановочного неравенства выражение
является максимально возможным значением скалярного произведения рассматриваемых последовательностей. Суммируя неравенства
получаем
или, разделив на n2:
Непрерывный случай
Существует также непрерывный аналог неравенства Чебышева для сумм:
Если f(x) и g(x) — это вещественные интегрируемые на [0,1] функции, возрастающие или убывающие одновременно, то
Wikimedia Foundation. 2010.
Неравенство Чебышёва — В Википедии существует другое неравенство, носящее имя Чебышёва см. Неравенство Чебышёва для сумм. Неравенство Чебышёва, известное также как неравенство Биенэме Чебышева, это распространённое неравенство из теории меры и теории вероятностей. Оно… … Википедия
Неравенство Чебышёва (теория вероятностей) — Неравенство Чебышёва в теории вероятностей утверждает, что случайная величина в основном принимает значения близкие к своему среднему. Более точно, оно даёт оценку вероятности, что случайная величина примет значение далёкое от своего среднего.… … Википедия
Неравенство Чёбышева — Неравенство Чебышёва (теория вероятностей) Неравенство Чебышёва для сумм … Википедия
Чебышёв, Пафнутий Львович — Пафнутий Львович Чебышёв Дата рождения: 4 (16 мая) 1821 Место рождения: Окатово, Калужская губерния … Википедия
Чебышёв, Пафнутий — Пафнутий Львович Чебышёв Дата рождения: 4 (16 мая) 1821 Место рождения: Окатово, Калужская губерния … Википедия
Чебышёв П. — Пафнутий Львович Чебышёв Дата рождения: 4 (16 мая) 1821 Место рождения: Окатово, Калужская губерния … Википедия
Чебышёв Пафнутий Львович — Пафнутий Львович Чебышёв Дата рождения: 4 (16 мая) 1821 Место рождения: Окатово, Калужская губерния … Википедия
Чебышёв П. Л. — Пафнутий Львович Чебышёв Дата рождения: 4 (16 мая) 1821 Место рождения: Окатово, Калужская губерния … Википедия
Неравенство об одномонотонных последовательностях — Перестановочное неравенство, или неравенство об одномонотонных последовательностях, или «транс неравенство», утверждает, что скалярное произведение двух наборов чисел является максимальным возможным, если наборы одномонотонны (то есть оба… … Википедия
Чебышева неравенство — Неравенство Чебышёва (теория вероятностей) Неравенство Чебышёва для сумм … Википедия