- Функциональная зависимость
-
В данной статье приведено общее определение математической функции. В средних школах и на нематематических специальностях высших учебных заведениях изучают более простое понятие числовой функции, являющееся частным случаем математической функции.
Содержание
Определения
- Нестрогое определение: функция — это «закон», по которому каждому значению элемента x из некоторого множества X ставится в соответствие единственный элемент y из множества Y.
- Строгое определение: функция или отображе́ние — это бинарное отношение, обладающее свойством:
- Функция называется инъективной, если
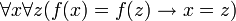
Обозначения
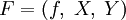 ,
, 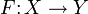 или
или 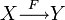 для отображения F множества X в множество Y;
для отображения F множества X в множество Y;
- Множество X называется о́бластью определе́ния отображения F (обозначается D(F), или
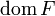 .).
.). - Множество Y называется о́бластью значе́ний отображения F.(обозначается E(F), или
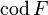 ).
).
- Множество X называется о́бластью определе́ния отображения F (обозначается D(F), или
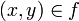 , y = F(x) или
, y = F(x) или 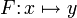 или
или 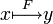 . Используется также обратная польская запись: y = xF, а иногда y = xF.
. Используется также обратная польская запись: y = xF, а иногда y = xF.
- Элементы x называют аргументами функции, а соответствующие элементы y — значениями функции.
Связанные определения
- Пусть дано отображение
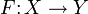 , и
, и 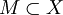 . Тогда суже́нием функции F на M называется функция
. Тогда суже́нием функции F на M называется функция 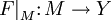 , определяемая равенством
, определяемая равенством
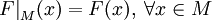 .
.- Это определение подчёркивает, что фиксация области определения является частью определения функции.
-
- F является продолжением функции
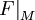 на множество
на множество 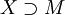 . Можно рассматривать продолжения, обладающие различными свойствами, например аналитическое продолжение.
. Можно рассматривать продолжения, обладающие различными свойствами, например аналитическое продолжение.
- F является продолжением функции
- Пусть
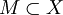 . Тогда о́бразом множества M называется подмножество множества Y, определяемое равенством
. Тогда о́бразом множества M называется подмножество множества Y, определяемое равенством
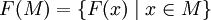 .
.
- Множество F(X) называется образом отображения F и обозначается
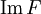 .
.
- Пусть задано отображение
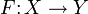 ,
, 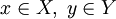 и y = F(x). Тогда x называется проо́бразом y, а y называется о́бразом x. Согласно определению отображения, каждый элемент
и y = F(x). Тогда x называется проо́бразом y, а y называется о́бразом x. Согласно определению отображения, каждый элемент  должен иметь ровно один образ, но элемент
должен иметь ровно один образ, но элемент 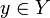 может не иметь прообразов либо иметь один или несколько.
может не иметь прообразов либо иметь один или несколько.
- Например, пусть дана функция
 , где F(x) = x2. Тогда
, где F(x) = x2. Тогда
- y = − 1 не имеет прообразов;
- y = 0 имеет единственный прообраз x = 0;
- y = 1 имеет два прообраза: x1 = 1 и x2 = − 1.
- Например, пусть дана функция
- Пусть задано отображение
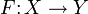 , и
, и 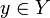 . Тогда множество
. Тогда множество 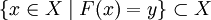 называется по́лным проо́бразом элемента y. Полный прообраз обозначается F - 1(y).
называется по́лным проо́бразом элемента y. Полный прообраз обозначается F - 1(y).
- Например, пусть
 , и F(x) = sinx. Тогда
, и F(x) = sinx. Тогда
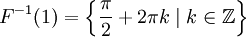 .
.
- Например, пусть
- Пусть
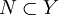 . Тогда проо́бразом множества N называется подмножество множества X, определяемое равенством
. Тогда проо́бразом множества N называется подмножество множества X, определяемое равенством
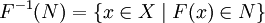 .
.
- Например, пусть
 , и F(x) = cosx. Тогда
, и F(x) = cosx. Тогда
![F\left(\left[0,\;\frac{\pi}{2}\right]\right)=[0,\;1]](/pictures/wiki/files/100/dba138bda54fabf61267657020bc6597.png) ,
,![F^{-1}([0,\;1])=\bigcup\limits_{n\in\Z}\left[-\frac{\pi}{2}+2\pi n,\;\frac{\pi}{2}+2\pi n\right]](/pictures/wiki/files/98/b08d3692d3671e4fbc9a70a52fc654a5.png) .
.
Свойства
Свойства прообразов и образов
 ;
;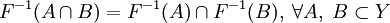 ;
;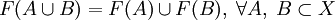 ;
;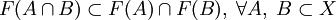 . Заметим отсутствие равенства в этом случае.
. Заметим отсутствие равенства в этом случае.
Классы функций
При необходимости можно различать отображения в зависимости от природы множеств X и Y. Если X и Y — числовые множества, такие, как
 или
или  , то отображение называют функцией. Если X или Y многомерны, например,
, то отображение называют функцией. Если X или Y многомерны, например,  или
или 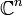 , то отображение называют ве́ктор-фу́нкцией. Если X — произвольной природы, а Y — поле, то отображение называют функциона́лом. В специальных случаях используют и другие термины: оператор, функтор, преобразование, морфизм и т. д.
, то отображение называют ве́ктор-фу́нкцией. Если X — произвольной природы, а Y — поле, то отображение называют функциона́лом. В специальных случаях используют и другие термины: оператор, функтор, преобразование, морфизм и т. д.Вариации и обобщения
Функции нескольких аргументов
Определение функции легко обобщить на случай функции многих аргументов.
Пусть даны множества
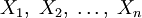 и множество Y, тогда упорядоченное множество всех кортежей
и множество Y, тогда упорядоченное множество всех кортежей 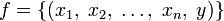 называется функцией n аргументов тогда и только тогда, когда для любых
называется функцией n аргументов тогда и только тогда, когда для любых 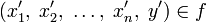 и
и 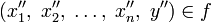 из
из 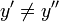 следует, что
следует, что ![x_{n}' \neq x_{n}'',\forall x\in [1,\;n]\cap\Z](/pictures/wiki/files/51/34b01413828b3a6b8b4f43b4c45d1446.png) .[1]
.[1]Примечания
- ↑ Кудрявцев Л. Д. Курс математического анализа. — том 1. — М.: Высшая школа, 1981. — с. 8.
См. также
- Композиция функций
- График функции
- Сюръективность
- Инъективность
- Биективность
- Функция с множеством значений {0, 1}
- Функциональное уравнение
Литература
- Функция. Математический энциклопедический словарь. — Гл. ред. Ю. В. Прохоров. — М.: «Большая российская энциклопедия», 1995.
Wikimedia Foundation. 2010.

