- Функция Гранди
-
Функция Гранди — функция, определённая для игр для 2 игроков, где проигрывает игрок, не имеющий возможности сделать очередной ход. Широко используется в теории игр. В случае дискретных игр иногда называется нимбером.
Функция определена на множестве всех позиций игры G следующим образом:
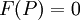 ,
если позиция P - однозначно проигрышная (нельзя сделать ни одного хода)
,
если позиция P - однозначно проигрышная (нельзя сделать ни одного хода)
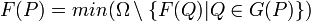 в иных случаях(здесь Ω - множество целых неотрицательных чисел,
а G(P) - множество всех допустимых ходов из позиции P)
в иных случаях(здесь Ω - множество целых неотрицательных чисел,
а G(P) - множество всех допустимых ходов из позиции P)
Применение
Одно из полезных свойств функции Гранди заключается в том, что она равна нулю для всех проигрышных позиций и положительна для всех выигрышных позиций. Это даёт метод нахождения выигрышной стратегии:
- Найти функцию Гранди, например, строя её рекуррентно, начиная с конечных позиций.
- Если в начальной позиции функция Гранди равна нулю, то игра для первого игрока проигрышна.
- В противном случае, первый игрок может выиграть, перемещаясь каждым ходом в позицию с нулевым значением функции Гранди.
Сумма игр
Если у нас имеется n игр G1,G2,...,Gn, то можно рассмотреть комбинацию этих игр, для которой игровое поле состоит из совокупности игровых полей для игр G1,G2,...,Gn и за один ход игрок может выбрать некоторое i, 1 ≤ i ≤ n, и сделать ход на игровом поле для игры Gi. Такая комбинация называется суммой игр G1,G2,...,Gn и обозначается G1 + G2 + ... + Gn. Ситуацию на игровом поле игры G1 + G2 + ... + Gn, когда игровое поле игры Gi находится в позиции Pi, удобно обозначать как (P1,P2,...,Pn).
Функция Гранди обладает одним удивительным свойством, которое позволяет оптимально играть в сумму игр G1 + G2 + ... + Gn, зная функцию Гранди для всех позиций каждой из игр Gi. Формулируется оно следующим образом:
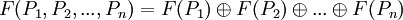 , где
, где 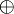 — исключающее «или».
— исключающее «или».Ссылки
1. Куммер Б.N. «Игры на графах», 1982 (§ 2.2. Функция Гранди и суммы порядка р)
2. http://yucs.org/~gnivasch/cgames/spraguegrundy/index.html Статья о теории Шпрага-Гранди объективных игр на графах (на англ. яз.)
Wikimedia Foundation. 2010.
