Вписанный угол

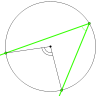
Вписанный угол — термин планиметрии; обозначает угол, вершина которого лежит на окружности, а обе стороны пересекают эту окружность.

Свойства

• Теорема о вписанном угле:

Вписанный угол равен половине центрального угла, опирающегося на ту же дугу, и равен половине дуги, на которую он опирается, либо дополняет половину центрального угла до 180°.

Доказательство  

Пусть $\angle ABC$ — вписанный угол окружности с центром $O$, опирающийся на дугу $AC$. Докажем, что $\angle ABC = \angle AOC/2$. Рассмотрим три возможных случая расположения луча ВО относительно угла АВС.

1. Луч $BO$ совпадает с одной из сторон $\angle ABC$, например со стороной $BC$. В этом случае дуга $AC$ меньше полуокружности, поэтому $\angle AOC = AC$. Так как $\angle AOC$ — внешний угол равнобедренного $\triangle ABO$, а углы при основании равнобедренного треугольника равны, один из них это $\angle ABC$, значит их сумма равна $2\angle ABC$, a $\angle AOC = 2\angle ABC$. Отсюда следует, что $\angle ABC = 0{,}5\angle AOC$.

2. Луч $BO$ делит $\angle ABC$ на два угла. В этом случае луч $BO$ пересекает дугу $AC$ в некоторой точке $D$. Точка $D$ разделяет дугу $AC$ на две дуги: $AD$ и $DC$. По доказанному в п.1 $\angle ABD = 0{,}5AD$ и $\angle DBC = 0{,}5DC$. Складывая эти равенства почленно, получаем: $\angle ABD + \angle DBC = 0{,}5AD+0{,}5DC$, или $\angle ABC = 0{,}5AC$.

3. Луч $BO$ лежит вне $\angle ABC$. В этом случае дуга $AC$ составляет часть дуги $AD$. По доказанному в п.1 $\angle ABD = 0{,}5AD$ и $\angle DBC = 0{,}5DC$. $\angle ABC = \angle ABD - \angle DBC = 0{,}5AD-0{,}5DC = 0{,}5(AD-DC)$. Т.к. дуга $AC=AD-DC$, то $\angle ABC = 0{,}5AC$.

• Следствия:
  

  Через вершину треугольника проведена касательная к описанной окружности
  • Вписанные углы, опирающиеся на одну дугу, равны.
  • Угол, опирающийся на диаметр, — прямой.
    • Гипотенуза прямоугольного треугольника является диаметром описанной около него окружности.
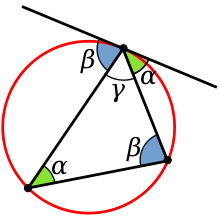
• Угол между касательной и хордой является предельным случаем вписанного угла и также равен половине дуги, на которую опирается.
• Угол между двумя хордами равен полусумме дуг, заключенных между хордами.

Для улучшения этой статьи по математике желательно?: Найти и оформить в виде сносок ссылки на авторитетные источники, подтверждающие написанное.