Обнаружение с использованием оптимальной фильтрации

Обнаружение с использованием оптимальной фильтрации

5.6. Обнаружение с использованием оптимальной фильтрации

5.6.1. ЭС обнаружения на ЧВФ

На основе ЧВФ рассмотрим функциональную схему ЭС обнаружения, изображенную на рис. 5.14.

Файл:514.png

Рис.514.
Функциональная схема ОиЛзЭС обнаружения с предварительной фильтрацией сигнала:
СПОИ - система первичной обработки информации; фл - бесшумный линейный ЧВФ; ПУ - пороговое устройство

    Аддитивная смесь полезного сигнала и фоновой помехи, приходящая на вход системы первичной обработки информации (СПОИ), преобразуется этой системой в некоторую одномерную реализацию 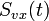$S_{vx}(t) \,\!$, являющуюся функцией времени и представляющую собой электрический сигнал, снимаемый с ПИ. В силу линейности СПОИ реализация 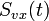$S_{vx}(t) \,\!$ состоит из суммы полезного сигнала 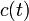${c(t)} \,\!$ и помехи 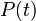$P(t) \,\!$ , которая учитывает как фоновую помеху, так и собственный шум ПИ. Вид реализации также изображен на рис. 5.14, где штриховой кривой показан полезный сигнал, пиковое значение которого соответствует времени 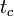$t_c \,\!$. Поскольку момент появления цели в мгновенном угловом поле ОиЛзЭС неизвестен, то время 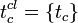$t_c^{cl} = \{t_c\} \,\!$ является случайной величиной.

    Реализация 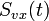$S_{vx}(t) \,\!$ поступает на вход нешумящего линейного ЧВФ, имеющего ПФ 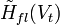$\tilde{H}_{fl}(V_t) \,\!$, на выходе которого формируется реализация 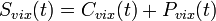$S_{vix}(t) = C_{vix}(t) + P_{vix}(t) \,\!$. ПУ выдает решение по методу однократного отсчета, непрерывно сравнивая мгновенное значение реализации 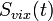$S_{vix}(t) \,\!$ с порогом, рассчитанным в соответствии с одним из критериев качества. Таким образом, все формулы для расчета вероятностных характеристик обнаружения, полученные в пп. 5.1 – 5.4, остаются в силе. Надо только установить значения необходимых для расчета параметров полезного сигнала и помехи на входе ПУ с учетом характеристик ЧВФ.

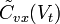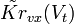Обозначив ЧВС полезного сигнала и энергетический ЧВС, помехи на входе ЧВФ через $\tilde{C}_{vx}(V_t) \,\!$ и $\tilde{Kr}_{vx}(V_t) \,\!$, а аналогичные ЧВС, корреляционную функцию и дисперсию помехи на выходе ЧВФ – через 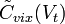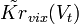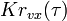$\tilde{C}_{vix}(V_t) \,\!$, $\tilde{Kr}_{vix}(V_t) \,\!$, $Kr_{vx}(\tau) \,\!$ и $\sigma^2_{vix} \,\!$.

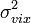    Сигнал запаздывает по отношению к началу реализации на время 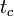$t_c \,\!$. Поэтому ЧВС сигнала на входе ЧВФ

$\tilde{C}_{vx}(V_t) = \tilde{C}(V_t)\exp(-i2\pi t_cv_t) \,\!$,

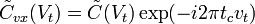        где 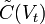$\tilde{C}(V_t) \,\!$ - ЧВС полезного сигнала для которого за начало отсчета времени принято $t = t_c \,\!$. Для ЧВС на выходе получим

$\tilde{C}_{vix}(V_t) = \tilde{C}_{vx}(V_t)\tilde{H}_{fl}(V_t) = \tilde{C}(V_t)\tilde{H}_{fl}(V_t)\exp(-i2\pi t_cv_t) \,\!$; $\tilde{Kr}_{vix}(V_t) = \tilde{Kr}_{vx}(V_t)| \tilde{H}_{fl}(V_t) |^2 \,\!$.

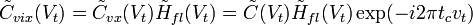    Для полезного сигнала, корреляционной функции и дисперсии помехи на выходе ЧВФ имеем

$C_{vix}(t) = F^{-1} \{ \tilde{C}_{vix}(v_t) \} = \int_{-\infty}^{\infty} \tilde{C}(v_t) \tilde{H}_{fl}(v_t) \exp [i2\pi (t - t_c)v_t] dv_t \,\!$; (5.59)

$Kr_{vix}(\tau) = F^{-1}\{ \tilde{Kr}_{vx}(v_t)\} = \int_{-\infty}^{\infty} \tilde{Kr}_{vx}(v_t) | \tilde{H}_{fl}(v_t) |^2 \exp [i2\pi \tau v_t]dv_t \,\!$; (5.60)

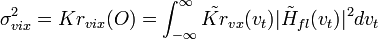$\sigma_{vix}^2 = Kr_{vix}(O) = \int_{-\infty}^{\infty} \tilde{Kr}_{vx}(v_t) | \tilde{H}_{fl}(v_t) |^2 dv_t \,\!$. (5.61)

5.6.2. Оценка мгновенного значения ОСП на выходе ЧВФ

    Найдем функцию 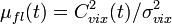$\mu_{fl}(t) = C_{vix}^2(t)/ \sigma_{vix}^2 \,\!$ , которую можно рассматривать как зависимость мгновенного значения ОСП от времени. Из (5.59) и (5.61) получим

$\mu_{fl}(t) = \frac{\left \{ \int_{-\infty}^{\infty} \tilde{C}(v_t) \tilde{H}_{fl}(v_t) \exp [i2\pi (t-t_c)v_t]dv_t \right \}^2 }{ \int_{-\infty}^{\infty} \tilde{Kr}_{vx}(v_t) | \tilde{H}_{fl}(v_t) |^2 dv_t } \,\!$. (5.62)

Используя неравенство Шварца-Буняковского

$\Bigl | \int_{-\infty}^{\infty} A(v_t)B(v_t)dv_t \Bigr |^2 \leq \int_{-\infty}^{\infty} | A(v_t) |^2 dv_t \int_{-\infty}^{\infty} | B(v_t)|^2 dv_t \,\!$ ,

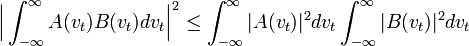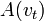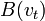где $A(v_t) \,\!$ и $B(v_t) \,\!$ - произвольные комплексные функции временной частоты $v_t \,\!$ и, полагая в нем

$A(v_t) = \sqrt{\tilde{Kr}_{vx}(v_t)} \tilde{H}_{fl}(v_t) \exp [i2\pi (t-t_c)v_t] \,\!$;

$B(v_t) = \tilde{C}(v_t)/ \sqrt{ \tilde{Kr}_{vx}(v_t) } \,\!$ ,

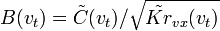получим

$\Bigl | \int_{-\infty}^{\infty} \tilde{c}(v_t) \tilde{H}_{fl}(v_t) \exp [i2\pi (t-t_c)v_t]dv_t \Bigr |^2 \leq \,\!$

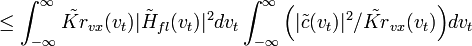$\leq \int_{-\infty}^{\infty} \tilde{Kr}_{vx}(v_t) | \tilde{H}_{fl}(v_t) |^2 dv_t \int_{-\infty}^{\infty} \Bigl ( |\tilde{c}(v_t)|^2 / \tilde{Kr}_{vx}(v_t) \Bigr ) dv_t \,\!$ . (5.63)

Откуда в соответствии с (5.62) имеем

$\mu_{fl}(t) = \mu(t) \leq \int_{-\infty}^{\infty} \Bigl [ |\tilde{c}(v_t)|^2 / \tilde{Kr}_{vx}(v_t) \Bigr ] dv_t \,\!$ .

    В итоге можно сделать важный вывод: ОСП на выходе линейного ЧВФ в произвольный момент времени не может быть больше величины

$\mu_{opt} = \mu(t) \leq \int_{-\infty}^{\infty} \Bigl [ |\tilde{c}(v_t)|^2 / \tilde{Kr}(v_t) \Bigr ] dv_t \,\!$ . (5.64)

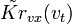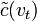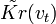    В формуле (5.64) для простоты опущен подстрочный индекс у $\tilde{Kr}_{vx}(v_t) \,\!$ , так что функции $\tilde{c}(v_t) \,\!$ и $\tilde{Kr}(v_t) \,\!$ определяют ЧВС полезного сигнала и энергетический ЧВС помехи на входе ЧВФ.

5.6.3. Синтез структурной схемы оптимального ЧВФ

    Теперь можно перейти к решению задачи синтеза структурной схемы оптимальной ОиЛзЭС обнаружения с позиции максимизации ОСП, т.е. к нахождению ПФ такого ЧВФ, который обеспечивает получение на его выходе оптимальное (максимальное) значение 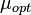$\mu_{opt} \,\!$ . Полагая в (5.62)

$\tilde{H}_{fl}(v_t) = K_{fl}[\tilde{c}*(v_t)/\tilde{Kr}_{vx}(v_t)] \exp (-i2\pi t_3v_t) \,\!$ , (5.64)

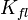где $K_{fl} \,\!$ - постоянный коэффициент, имеющий размерность спектра сигнала 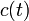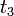$c(t) \,\!$; $t_3 \,\!$ - время запаздывания выходного сигнала ЧВФ по отношению к моменту действия входного сигнала, получим

$\mu_{fl}(t) = \frac{ \left \{ \int_{-\infty}^{\infty} \Bigl [ |\tilde{c}(v_t)|^2 / \tilde{Kr}_{vx}(v_t) \Bigl ] \exp [i2\pi (t-t_c-t_3)v_t]dv_t \right \}^2 }{ \int_{-\infty}^{\infty} \Bigl [ | \tilde{c}(v_t)|^2 / \tilde{Kr}_{vx}(v_t) \Bigr ] dv_t } \,\!$ (5.65)

Нетрудно заметить, что в момент времени 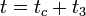$t = t_c + t_3 \,\!$ экспоненциальный член в числителе (5.65) обращается в единицу и ОСП на выходе ЧВФ 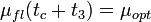$\mu_{fl}(t_c + t_3) = \mu_{opt} \,\!$ , т.е. максимально. Таким образом, ПФ оптимального ЧВФ

$\tilde{H}_{opt}(v_t) = K_{fl} [ \tilde{c} * (v_t) / \tilde{Kr}_{vx}(v_t) ] \exp (i2\pi t_3v_t) \,\!$ (5.66)

     Интеграл в числителе (5.65) определяет полезный сигнал на выходе оптимального ЧВФ. Равенство единице экспоненциального члена в подынтегральном выражении (5.59) означает, что в момент времени 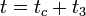$t = t_c + t_3 \,\!$ все спектральные составляющие сигнала находятся в одинаковой фазе. Следовательно, в этот момент времени полезный сигнал может быть получен простым суммированием амплитуд его спектральных составляющих, т.е. достигает максимального (пикового) значения.

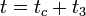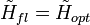     Из (5.59) при $t = t_c + t_3 \,\!$ и $\tilde{H}_{fl} = \tilde{H}_{opt} \,\!$ следует:

$c(t_c + t_3) = c_{vix}^{max} = K_{fl} \int_{-\infty}^{\infty} \Bigl [ | \tilde{c}(v_t)|^2 / \tilde{Kr}_{vx}(v_t) \Bigr ] dv_t = K_{fl} \mu_{opt} \,\!$ , (5.67)

т.е. на выходе оптимального ЧВФ максимальное (пиковое) значение полезного сигнала численно равно произведению $K_{fl} \mu_{opt} \,\!$ .

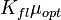     Корреляционную функцию помехи на выходе оптимального ЧВФ найдем из (5.60) при 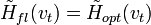$\tilde{H}_{fl}(v_t) = \tilde{H}_{opt}(v_t) \,\!$. Учитывая, что 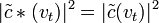$|\tilde{c}*(v_t)|^2 = |\tilde{c}(v_t)|^2 \,\!$ , получим

$Kr_{vix}(\tau) = K_{fl}^2 \int_{-\infty}^{\infty} \Bigl [ | \tilde{c}(v_t)|^2 / \tilde{Kr}_{vx}(v_t) \Bigr ] \exp [i2\pi \tau v_t]dv_t \,\!$ .

Дисперсия помехи на выходе оптимального ЧВФ

$\sigma_{vix}^2 = Kr_{vix}(O) = K_{fl}^2 \int_{-\infty}^{\infty} \Bigl [ |\tilde{c}(v_t)|^2 / \tilde{Kr}_{vx}(v_t) \Bigr ] dv_t = K_{fl}^2 \mu_{opt} \,\!$ . (5.68)

     Таким образом, дисперсия помехи на выходе оптимального ЧВФ численно равна произведению 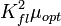$K_{fl}^2 \mu_{opt} \,\!$ . Деление выражения (5.67), возведенного в квадрат, на (5.68) дает

$\left ( C_{vix}^{max} \right )^2 / \sigma_{vix}^2 = \left ( K_{fl} \mu_{opt} \right )^2 / \left ( K_{fl}^2 \mu_{opt} \right ) = \mu_{opt} \,\!$ .

     Для определения вероятностных характеристик ОиЛзЭС обнаружения на основе оптимальной фильтрации следует использовать выражения (5.26), (5.29) – (5.32), (5.37), (5.41), (5.43) – (5.45) при 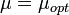$\mu = \mu_{opt} \,\!$ и

$\bar v_{p} = \frac{ \sqrt{-Kr''(O)} }{ 2\pi \sigma } = \Bigl[ \frac{1}{\mu_{opt}} \int_{-\infty}^{\infty} \Bigl[ | \tilde{c}(v_t)|^2 / \tilde{Kr}_{vx}(v_t) \Bigr] dv_t \Bigr]^{\frac{1}{2}} \,\!$ (5.69)

     Если помеха на входе ЧВФ имеет вид белого шума, т.е. 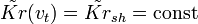$\tilde{Kr}(v_t) = \tilde{Kr}_{sh} = \mbox{const} \,\!$ , то из (5.64) имеем

$\mu_{opt} = \Bigl[ \int_{-\infty}^{\infty} |\tilde{c}(v_t)|^2 dv_t \Bigr] / SH_0 \,\!$ .

     На основании равенства Парсеваля

$\int_{-\infty}^{\infty} |\tilde{c}(v_t)|^2 dv_t = \int_{-\infty}^{\infty} |\tilde{c}(t)|^2 dt = W_s \,\!$ ,

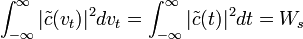так что $\mu_{opt} = W_s / SH_0 \,\!$ .

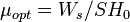     Таким образом, при белом шуме обнаружение объекта на основе оптимальной фильтрации и корреляционный метод приводит к одинаковому результату [см. (5.56)].

     Аналогично модуляционной передаточной функции на основе (5.66), т.е. МПФ, называемой также амплитудно-частотной характеристикой (АЧХ) оптимального ЧВФ и пропорциональной отношению 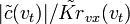$|\tilde{c}(v_t)| / \tilde{Kr}_{vx}(v_t) \,\!$ , показывает, что фильтр можно представить в виде двух последовательно включенных звеньев. Первое звено – помехоподавляющее с МПФ вида $\Bigl[ K_{fl} / \tilde{Kr}_{vx}(v_t) \Bigr] \,\!$ , коэффициент усиления которого обратно пропорционален энергетической спектральной плотности помехи. Второе звено с МПФ вида играет роль согласованного ЧВФ, обеспечивающего преимущественное пропускание тех гармоник, амплитуды которых в ЧВС входного сигнала имеют наибольшие значения.

     При реальных входных ЧВС полезного сигнала и помехи МПФ или АЧХ оптимального ЧВФ имеет достаточно сложную форму. Её практическая реализация, т.е. создание оптимального ЧВФ на современной элементарной базе, как правило встречает серьёзные затруднения. Однако это нисколько не умаляет практического значения теории оптимальной фильтрации. Рассчитав МПФ оптимального ЧВФ, всегда можно поставить задачу создания реального фильтра с МПФ, в той или иной степени близкой к оптимальной. Такой фильтр иногда называют подоптимальным.

     Характеристики качества любого линейного ЧВФ (в том числе и подоптимального) может служить величина

$\eta = \mu_{fl} / \mu_{opt} \,\!$ ,

показывающая, во сколько раз ОСП 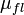$\mu_{fl} \,\!$ на выходе этого ЧВФ меньше отношения 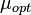$\mu_{opt} \,\!$ на выходе оптимального ЧВФ. Таким образом, величина 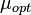$\mu_{opt} \,\!$ выступает здесь в качестве меры потенциальной возможности выделения сигнала из его смеси с помехой при линейной фильтрации, т.е. меры потенциальной помехозащищенности ОиЛзЭС обнаружения.

5.6.4. Анализ оптимального ОСП

     В результате из анализа (5.64) следует:

1. ОСП на выходе оптимального ЧВФ выражается через ЧВС полезного сигнала и помехи на входе фильтра, т.е. учитывает все их энергетические признаки;
2. Если в спектре полезного сигнала пренебречь гармониками на некотором участке ЧВС, то 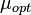$\mu_{opt} \,\!$ уменьшается, несмотря на то что на этом участке спектра сигнал может быть много слабее помехи;
3. Если в какой-либо области ЧВС сигнала помеха отсутствует, то 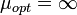$\mu_{opt} = \infty \,\!$ . Это объясняется тем, что, в соответствии с (5.66) в диапазоне временных частот, где сигнал есть, а помеха отсутствует, МПФ или АЧХ оптимального ЧВФ неограниченно возрастает, т.е. уровень полезного сигнала на выходе фильтра стремится к бесконечности. Можно представить оптимальный ЧВФ и в несколько ином виде, когда его МПФ в указанном диапазоне частот конечна и имеет любую форму. Вне этого диапазона МПФ тождественно равна нулю. В этом случае уровень сигнала на выходе ЧВФ также конечен, однако помеха подавляется полностью и поэтому 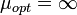$\mu_{opt} = \infty \,\!$ . Естественно, что подобное сочетание ЧВС полезного сигнала и помехи на практике не встречается и рассматриваемый случай имеет лишь теоретическое значение;
4. Помеха в том диапазоне частот, где сигнал имеет наибольшую интенсивность, снижает 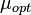$\mu_{opt} \,\!$ наиболее сильно. Поэтому наиболее существенное значение для увеличения 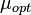$\mu_{opt} \,\!$ имеют те частотные области, в которых сигнал в наибольшей мере превосходит помеху;
5. Если перед поступлением на вход оптимального ЧВФ реализация пропускается через линейный нешумящий ЧВФ, то это никак не повлияет на 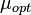$\mu_{opt} \,\!$ . Изменится лишь ПФ оптимального ЧВФ;
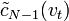6. Если ОиЛзЭС обработки может быть представлена в виде $N \,\!$ последовательных линейных нешумящих звеньев (рис. 5.15), причем последнее звено реализовано в виде оптимального ЧВФ по отношению к действующим на его входе полезному сигналу с ЧВС $\tilde{c}_{N-1}(v_t) \,\!$ и помехе с энергетическим ЧВС 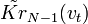$\tilde{Kr}_{N-1}(v_t) \,\!$ , то весь тракт является оптимальным ЧВС по отношению к его входному воздействию.

Файл:515.png

Рис.515.
Функциональная схема ОиЛзЭС обработки сигнала в виде оптимального ЧВФ с последним звеном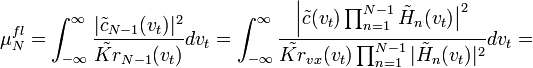

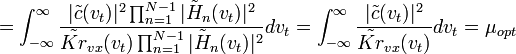$\mu_N^{fl} = \int_{-\infty}^{\infty} \frac{ |\tilde{c}_{N-1}(v_t)|^2 }{ \tilde{Kr}_{N-1}(v_t) } dv_t = \int_{-\infty}^{\infty} \frac{ \Bigl| \tilde{c}(v_t) \prod^{N-1}_{n=1}\tilde{H}_n(v_t) \bigr|^2 }{ \tilde{Kr}_{vx}(v_t) \prod^{N-1}_{n=1} | \tilde{H}_n(v_t)|^2 } dv_t = \,\!$

$= \int_{-\infty}^{\infty} \frac{ |\tilde{c}(v_t)|^2 \prod_{n=1}^{N-1} |\tilde{H}_n(v_t)|^2 }{ \tilde{Kr}_{vx}(v_t) \prod_{n=1}^{N-1} |\tilde{H}_n(v_t)|^2 } dv_t = \int_{-\infty}^{\infty} \frac{ |\tilde{c}(v_t)|^2 }{ \tilde{Kr}_{vx}(v_t) } dv_t = \mu_{opt} \,\!$ .

Поэтому вне зависимости от вида ПФ всех предшествующих (N-1) звеньев последнее звено корректирует ПФ всего тракта обработки, превращая его в оптимальный ЧВФ по отношению к входному воздействию, характеризующемуся ЧВС 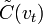$\tilde{C}(v_t) \,\!$ и $\tilde{Kr}(v_t) \,\!$ .

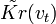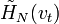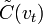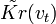     Очевидно, что ПФ $\tilde{H}_N(v_t) \,\!$ последнего (корректирующего) звена при заданных входных ЧВС $\tilde{C}(v_t) \,\!$ и $\tilde{Kr}(v_t) \,\!$ будет зависеть от вида ПФ всех предшествующих звеньев.

     В том случае, когда одно или несколько звеньев тракта обработки вносят дополнительные шумы, оптимизация тракта по отношению к его входному воздействию не может быть выполнена. Получаемое на выходе тракта ОСП будет меньше 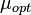$\mu_{opt} \,\!$. Действительно, предположим, что шум, статистически независимый от внешней помехи, вносит звено с индексом m. Обозначим энергетический ЧВС шума, приведенного ко входу m-го звена, через 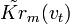$\tilde{Kr}_m(v_t) \,\!$ . Тогда ЧВС суммарной помехи на входе m-го звена

$\tilde{Kr}_m^{\sum}(v_t) = \tilde{Kr}_{vx}(v_t) \prod_{n=1}^{m-1} |\tilde{H}_n(v_t)|^2 + \tilde{Kr}_m(v_t) \,\!$ ,

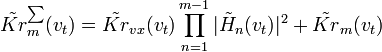и

$\tilde{Kr}_{N-1}(v_t) = \tilde{Kr}_m^{\sum}(v_t) \prod_{n=m}^{N-1} |\tilde{H}_n(v_t)|^2 = \tilde{Kr}_{vx}(v_t) \prod_{n=1}^{N-1} |\tilde{H}_n(v_t)|^2 + \tilde{Kr}_m(v_t) \prod_{n=m}^{N-1} |\tilde{H}_n(v_t)|^2 \,\!$

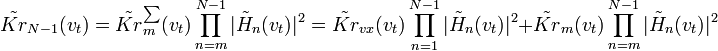
ОСП на выходе электронного тракта при оптимизированном последнем звене

$\mu_{it} = \int_{-\infty}^{\infty} \frac{ |\tilde{c}_{N-1}(v_t)|^2 }{ \tilde{Kr}_{N-1}(v_t) }dv_t = \int_{-\infty}^{\infty} \frac{ \Bigl| \tilde{c}(v_t) \prod_{n=1}^{N-1} \tilde{H}_n(v_t) \Bigr|^2 }{ \tilde{Kr}_{vx}(v_t) \prod_{n=1}^{N-1} |\tilde{H}_n(v_t)|^2 + \tilde{Kr}_m(v_t) \prod_{n=m}^{N-1} |\tilde{H}_n(v_t)|^2 }dv_t \,\!$ ,

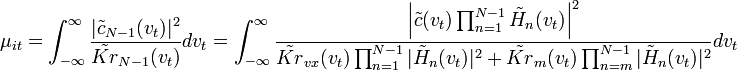откуда следует, что 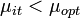$\mu_{it} < \mu_{opt} \,\!$ . Равенство 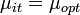$\mu_{it} = \mu_{opt} \,\!$ имеет место только при $\tilde{Kr}_m(v_t) = O \,\!$ .

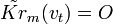5.6.5. Оптимальная фильтрация в оптической изображающей системе

     Оптимальная фильтрация, рассмотренная в применении к одномерным входным воздействиям, являющимся функциями времени, может быть распространена на многомерные сигналы. Для ОиЛзЭС характерными входными воздействиями являются двумерное поле яркости 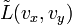$\tilde{L}(v_x, v_y) \,\!$ и фоновая помеха с пространственной спектральной плотностью 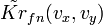$\tilde{Kr}_{fn}(v_x, v_y) \,\!$ . ПФ двумерного оптимального ПЧФ может быть получена, как и ранее, с использованием обобщенного неравенства Шварца-Буняковского:

$\tilde{H}_{opt}(v_x, v_y) = K_{fl} [ \tilde{L}*(v_x, v_y) / \tilde{Kr}_{fn}(v_x, v_y) ] \exp (-i2\pi (x_c v_x + y_c v_y)) \,\!$ ,

где ОСП на выходе ПЧФ

$\mu_{opt} = \int \int_{-\infty}^{\infty} \Bigl[ |\tilde{L}(v_x, v_y)|^2 / \tilde{Kr}_{fn}(v_x, v_y) \Bigr] dv_x dv_y \,\!$ .

     Практическая реализация оптимального ПЧФ затруднена в ещё большей степени, чем ЧВФ. Причиной этого является ограниченная разрешающая способность ОиЛзЭС и ПИ, а также шумы последнего, которые могут являться доминирующими. ^[1] Если временная оптимальная фильтрация позволяет оценить потенциальную помехозащищенность ОиЛзЭС, «испорченную» несовершенством системы первичной отработки информации (двумерным оптическим трактом), то представление ОИзС в виде оптимального ПЧФ дает возможность получить действительный предел помехозащищенности. Результаты исследований влияния пространственных характеристик фона на ОСП на выходе двумерного оптимального ПЧФ изложены в работе [24].

5.6.6. Трёхмерный оптимальный пространственно-временной ЧФ

     Для оценки возможностей приема оптических сигналов, изменяющихся не только в пространстве, но и во времени, может быть использована ПФ трехмерного оптимального пространственно-временного частотного фильтра [24]:

$\tilde{H}_{opt}(v_x, v_y, v_t) = [\tilde{L}*(v_x, v_y, v_t) / \tilde{Kr}_{fn}(v_x, v_y, v_t)] \exp (-i2\pi (x_c v_x + y_c v_y + t_a v_t)) \,\!$ ;

$\mu_{opt} = \int \int_{-\infty}^{\infty} \int \Bigl[ |\tilde{L}(v_x, v_y, v_t)|^2 / \tilde{Kr}_{fn}(v_x, v_y, v_t) \Bigr] dv_x dv_y dv_t \,\!$ .

Примечания

1. ↑ Напомним, что теоретически оптимальный фильтр должен быть бесшумным. В отношении ЧВФ это условие хотя бы приближенно выполняется, так как возможно создание электронного тракта, шумы которого значительно меньше суммы собственных шумов ПИ и фоновой помехи. В то же время могут иметь место такие условия работы ОЭС, в которых шум ПИ превышает фоновую помеху.

Связать^?