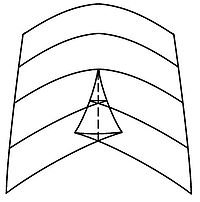
Ласточкин хвост (поверхность)

У этого термина существуют и другие значения, см. Ласточкин хвост.

Ла́сточкин хвост (англ. swallow tail) — нерегулярная поверхность в трёхмерном пространстве, определить которую можно несколькими эквивалентными способами. Рассмотрим многочлен $P(x)=x^4+ax^2+bx+c$ от переменной $x$, зависящий от коэффициентов $a,b,c$ (и переменная, и коэффициенты предполагаются вещественными). Каждой тройке коэффициентов $a,b,c$ однозначно соответствует многочлен $P(x)$, а также точка в пространстве с декартовыми координатами $(a,b,c)$. Тогда «ласточкин хвост» определяется как поверхность $S$ в пространстве с координатами $(a,b,c)$, точкам которой соответствуют многочлены $P(x)$, имеющие кратные корни.

«Ласточкин хвост»

Поверхность $S$ имеет особенность в виде ребра возврата и линии самопересечения, при этом ребро возврата имеет вид полукубической параболы, имеющей особенность в виде точки возврата (каспа). Поверхность $S$ разбивает пространство $(a,b,c)$ на три области, соответствующие числу вещественных корней многочлена $P(x)$. Именно, в области, имеющей вид криволинейной пирамиды, ребрами которой являются линия самопересечения и две ветви полукубической параболы, $P(x)$ имеет 4 вещественных корня; в прилегающей к ней области — два и в оставшейся области — нуль.

Ласточкин хвост находит многочисленные применения в теории катастроф и теории бифуркаций. В частности, он является поверхностью критических значений (образом множества критических точек) одного из устойчивых ростков гладких отображений $f: \R^3\to\R^3$. Ласточкин хвост является стратифицированным многообразием.

Параметрическое задание

Пользуясь данным определением, можно получить формулу, задающую ласточкин хвост параметрически:

$\left\{ \begin{matrix} x_1(u,v) =& u \\ x_2(u,v) =& 2v^3 + uv \\ x_3(u,v) =& 3v^4 + uv^2. \\ \end{matrix} \right.$

Интересные факты

Поверхность ласточкин хвост была подробно изучена Кронекером в 1878 году, она встречается также в работах Кэли того же времени, посвящённых особенностям распространяющихся волновых фронтов и каустик. ^[1]

В 1983 году испанский художник Сальвадор Дали под впечатлением от работ французского математика Рене Тома в области теории катастроф написал картину «Ласточкин хвост», представляющую собой простую каллиграфическую композицию на светлом фоне, в центре которой изображено сечение поверхности $S$ в пространстве $(a,b,c)$ плоскостью $a = const >0$ — кривая с точкой самопересечения и двумя полукубическими точками возврата. На этой картине, ставшей последним произведением художника, можно видеть также кубическую параболу, стилизованные знаки интеграла и фрагменты музыкальных инструментов.^{[2] [3] [4] [5]}

Литература

• Арнольд В. И. Теория катастроф, — Любое издание.
• Арнольд В. И., Варченко А. Н., Гусейн-Заде С. М. Особенности дифференцируемых отображений, — Любое издание.
• Брус Дж., Джиблин П. Кривые и особенности: Геометрическое введение в теорию особенностей, — М.: Мир, 1988.
• Арнольд В. И. Особенности каустик и волновых фронтов, — М.: Фазис, 1996.
• В. И. Арнольд, В. С. Афраймович, Ю. С. Ильяшенко, Л. П. Шильников. Теория бифуркаций.

Примечания

1. ↑ Брус Дж., Джиблин П. Кривые и особенности: Геометрическое введение в теорию особенностей. — стр. 8.
2. ↑ Ласточкин хвост — последнее произведение Сальвадора Дали.
3. ↑ Дали Сальвадор. Биография.
4. ↑ The Swallow’s Tail
5. ↑ Dalí, Salvador, ‘Gala, Velásquez and the Golden Fleece’ (9 May 1979). Reproduced in-part in Robert Descharnes, Dalí, the Work, the Man (New York: Harry N. Abrams, 1984) 420. Originally published in French as Dalí, l’oeuvre et l’homme (Lausanne: Edita, 1984).