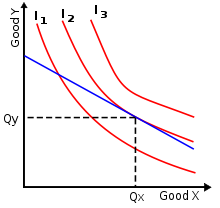
Бюджетная прямая

Бюджетная прямая, где:$A=\frac{m}{P_y}$ и $B=\frac{m}{P_x}$

Бюджетная прямая (Линия Бюджетных Oграничений, англ. Budget constraint) — показывает различные комбинации двух благ, которые потребитель может приобрести, если его денежный доход имеет фиксированную величину. Точки на линии отражают предельные возможности, обусловленные ограниченностью бюджета потребителя. Теория потребительского выбора использует концепцию бюджетных ограничений наряду с Кривoй безразличия для анализа потрeбительского выбора.

Уравнение прямой бюджетного ограничения (т.e. ограничения покупательной способности потребителя величиной его денежного дохода), в упрощённом случае выбора между двумя видами товаров, можно обобщить уравнением :

$m=P_x x+P_y y$

Где:

• $m=$ денежный доход (та его часть, идущая на потребительские траты)
• $P_x=$ цена конкретного товара
• $P_y=$ цена всех прочих товаров
• $x=$ количество приобретаемого товара
• $y=$ количество приобретаемыx прочих товаров

Индивид будет потреблять в (Qx, Qy).

Примечания

Для улучшения этой статьи желательно?: Проверить достоверность указанной в статье информации. Добавить иллюстрации. Дополнить статью (статья слишком короткая либо содержит лишь словарное определение). Найти и оформить в виде сносок ссылки на авторитетные источники, подтверждающие написанное. Викифицировать статью.