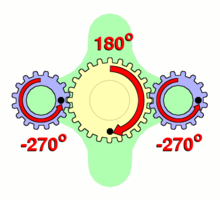
- Планетарная передача
-
Планетарная передача (дифференциальная передача) — механическая система, состоящая из нескольких планетарных зубчатых колёс (шестерён), вращающихся вокруг центральной, солнечной, шестерни. Обычно планетарные шестерни фиксируются вместе с помощью водила. Планетарная передача может также включать дополнительную внешнюю кольцевую (коронную) шестерню, имеющую внутреннее зацепление с планетарными шестернями.
Содержание
Передаточное отношение
Передаточное отношение такой передачи визуально определить достаточно сложно, в основном, потому что система может приводиться во вращение несколькими разными способами. Основными элементами планетарной передачи можно считать следующие:
- Солнечная шестерня: находится в центре;
- Водило: жёстко фиксирует друг относительно друга оси нескольких планетарных шестерён (сателлитов) одинакового размера, находящихся в зацеплении с солнечной шестерней;
- Кольцевая шестерня: внешнее зубчатое колесо, имеющее внутреннее зацепление с планетарными шестернями.
При использовании планетарной передачи в качестве редуктора один из трёх её основных элементов фиксируется неподвижно, другой элемент используется как ведущий, а третий — в качестве ведомого. Таким образом, передаточное отношение будет зависеть от количества зубьев каждого компонента, а также того, какой элемент закреплён.
Часто планетарные передачи используются для суммирования двух потоков мощности (например, планетарные ряды двухпоточных трансмиссий некоторых танков и др. гусеничных машин), в этом случае неподвижно зафиксированных элементов нет. Например, два потока мощности могут подводиться к солнечной шестерне и эпициклу, а результирующий поток снимается с водила.
Рассмотрим случай, когда водило зафиксировано, а мощность подводится через солнечную шестерню. В этом случае планетарные шестерни вращаются на месте со скоростью, определяемой отношением числа их зубьев относительно солнечной шестерни. Например, если мы обозначим число зубьев солнечной шестерни как S, а для планетарных шестерён примем это число как P, то передаточное отношение будет определяться формулой
 , то есть если у солнечной шестерни 24 зуба, а у планетарных по 16, то передаточное отношение будет -24/16, или -3/2, что означает поворот планетарных шестерён на 1,5 оборота в противоположном направлении относительно солнечной.
, то есть если у солнечной шестерни 24 зуба, а у планетарных по 16, то передаточное отношение будет -24/16, или -3/2, что означает поворот планетарных шестерён на 1,5 оборота в противоположном направлении относительно солнечной.Далее вращение планетарных шестерён может передаваться кольцевой шестерне, с соответствующим передаточным числом. Если кольцевая шестерня имеет A зубьев, то оно будет вращаться с соотношением P/A относительно планетарных шестерён. (В данном случае перед дробью нет минуса, так как при внутреннем зацеплении шестерни вращаются в одну сторону). Например, если на кольцевой шестерне 64 зуба, то относительно приведённого выше примера это отношение будет равно 16/64, или 1/4. Таким образом, объединив оба примера, мы получим следующее:
- Один оборот солнечной шестерни даёт -S/P оборотов планетарных шестерён;
- Один оборот планетарной шестерни даёт P/A оборотов кольцевой.
В итоге, если водило заблокировано, общее передаточное отношение системы будет равно -S/A.
В случае, если закреплена кольцевая шестерня, а мощность подводится к водилу, передаточное отношение на солнечную шестерню будет больше единицы и составит 1+A/S.
Всё вышесказанное можно описать следующим выражением:
 ,
,где n — это параметр передачи, равный
 , то есть отношению числа зубьев солнечной и планетарных шестерён.
, то есть отношению числа зубьев солнечной и планетарных шестерён.Если закрепить кольцевую шестерню, а мощность подводить к солнечной шестерне, то мощность должна сниматься с водила. В этом случае передаточное отношение будет равно
 Это самое маленькое передаточное число, которое может быть получено в планетарной передаче. Такие передачи используются, например, в тракторах и строительной технике, где требуется большой крутящий момент на колёсах при невысокой скорости.
Это самое маленькое передаточное число, которое может быть получено в планетарной передаче. Такие передачи используются, например, в тракторах и строительной технике, где требуется большой крутящий момент на колёсах при невысокой скорости.Схемы и выходные скорости планетарных передач Схема Выходная скорость Схема Выходная скорость Схема Выходная скорость Схема Выходная скорость 








































![{\color{red} n} = {\color{blue} n} \left[1-\left( \frac {\color{magenta} n} {\color{blue} n} -1 \right) \frac{\color{magenta}z} {\color{red}z}\right]](a65b1f2476b954b2d6fa6294da8cab05.png)

![{\color{red} n} = {\color{blue} n} \left[1-\left( \frac {\color{magenta} n} {\color{blue} n} -1 \right) \frac{\color{magenta}z} {\color{red}z}\right]](a65b1f2476b954b2d6fa6294da8cab05.png)




Формула Виллиса
 , где
, где  — передаточное число при заблокированном водиле
— передаточное число при заблокированном водиле  ,
,  — скорость солнечной шестерни,
— скорость солнечной шестерни,  - скорость водила и
- скорость водила и  — скорость кольцевой шестерни. [1] [2]
— скорость кольцевой шестерни. [1] [2]Применение
Наиболее широкое применение принцип нашёл в планетарных редукторах, автомобильных дифференциалах, бортовых планетарных передачах ведущих мостов тяжёлых автомобилей, кроме того, используется в суммирующих звеньях кинематических схем металлорежущих станков, также в редукторах привода воздушных винтов турбовинтовых двигателей (ТВД) в авиации.
В современных устройствах могут использоваться каскады из нескольких планетарных передач для получения большого диапазона передаточных чисел. На этом принципе работают многие автоматические коробки передач.Во время Второй мировой войны была разработана особая конструкция планетарной передачи, которая использовалась для привода небольших радаров.
Кольцевая шестерня изготавливалась из двух частей, каждая толщиной в половину толщины других компонентов. Одна из этих половинок фиксировалась неподвижно и имела на 1 зуб меньше, чем вторая. В такой конструкции при полном обороте планетарных шестерён и нескольких оборотах солнечной шестерни, подвижное кольцо поворачивалось всего на 1 зуб. Таким образом, получалось очень высокое передаточное отношение при небольших габаритах.
Литература
- Антонов А. С., Артамонов Б. А., Коробков Б. М., Магидович Е. И. Планетарные передачи // Танк. — М.: Воениздат, 1954. — С. 422—429. — 607 с.
См. также
- Планетарный редуктор
- Циклоидальная передача — механическая передача, подобная планетарной
- Механический редуктор
- Зубчатые передачи
- Автоматическая коробка переключения передач
- Передача Симпсона
- Эпицикл
- en:Sun and planet gear
Примечания
- ↑ Bernd Künne Köhler/Rögnitz Maschinenteile 2. — Vieweg+Teubner Verlag, 2008. — С. 508. — ISBN 3835100920
- ↑ Berthold Schlecht Maschinenelemente 2: Getriebe, Verzahnungen und Lagerungen. — Pearson Studium, 2010. — С. 787. — ISBN 3827371465
Для улучшения этой статьи желательно?: - Проставив сноски, внести более точные указания на источники.
Категории:- Детали машин и механизмов
- Механические передачи
- Трансмиссия
- Гибридные автомобили
- Устройство автомобиля
- Устройство танка
- Устройство трактора
Wikimedia Foundation. 2010.