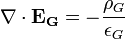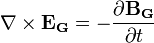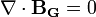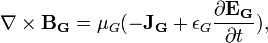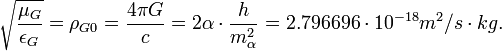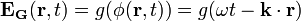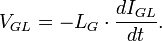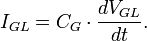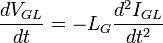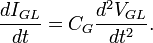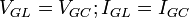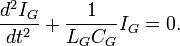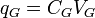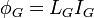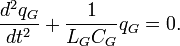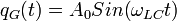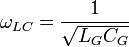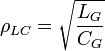Максвеллоподобные гравитационные уравнения

Максвеллоподобные гравитационные уравнения

В гравитации, Максвеллоподобные гравитационные уравнения составляют систему из четырех уравнений в частных производных, которые описывают свойства электроподобных и магнитоподобных гравитационных полей, а также их источников - зарядовой плотностью и плотностью тока. Эти уравнения используются с целью подтверждения того, что гравитационные волны подобно электромагнитным волнам имеют ту же скорость распространения, равную скорости света.

$\nabla \cdot \mathbf{E_G} = -\frac{\rho_G}{\epsilon_G} \$

$\nabla \times \mathbf{E_G} = -\frac{\partial \mathbf{B_G} }{\partial t } \$

$\nabla \cdot \mathbf{B_G} = 0 \$

$\nabla \times \mathbf{B_G} = \mu_G(-\mathbf{J_G} + \epsilon_G\frac{\partial \mathbf{E_G} }{\partial t }), \$

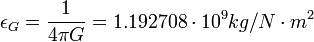где $\epsilon_G = \frac{1}{4\pi G} = 1.192708\cdot 10^9 kg/N\cdot m^2 \$ гравитоэлектрическая проницаемость (подобно электрической константе); G - гравитационная константа, c - скорость света в вакууме, и $\mu_G = \frac{4\pi G}{c^2} = 9.328772\cdot 10^{-27} n\cdot s^2/kg \$ гравитомагнитная восприимчивость (подобно магнитной константе). Из первого и четвертого уравнений можно получить волновое уравнение со следующей скоростью распространения волн:

$\frac{1}{\sqrt{\mu_G\epsilon_G}} = c = 2.99792458\cdot 10^8 m/s \$.

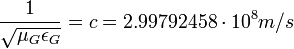Гравитационный характеристический импеданс свободного пространства может быть определен как:

$\sqrt{\frac{\mu_G}{\epsilon_G}} = \rho_{G0} = \frac{4\pi G}{c} = 2\alpha \cdot \frac{h}{m_{\alpha}^2} = 2.796696\cdot 10^{-18} m^2/s\cdot kg. \$

Также как и в электродинамике, характеристический импеданс играет доминирующую роль во всех процессах излучения и поглощения, подобно тому как согласовывается входной импеданс гравитационной антенны и импеданс свободного пространства. Численное значение этого импеданса очень мало и поэтому очень трудно сделать приемники гравитационного излучения с соответствующим согласованием импедансов.

История

Согласно Макдональду^[1] первым, кто использовал уравнения Максвелла при описании гравитации был Оливер Хевисайд^[2] Дело в том, что при слабом гравитационном поле стандартная теория гравитации может быть сведена к простым уравнениям типа Максвелла ^[3] Очевидно, что в 19-м столетии не было системы СИ, и поэтому первым упоминанием об гравидинамических константах возможно относится к Форварду (1961) ^[4] В 80-е годы максвеллоподобные гравитационные уравнениябыли использованы в монографии Валда по общей теории относительности ^[5] В 90-е годы этот подход использовал Саббата ^{[6] [7]}, а сегодня Раймонд Чиао ^{[8] [9] [10] [11]}, который разработал ряд путей по экспериментальному определению гравитационных волн используя холловские жидкости электронов при низких температурах.

Применения

Волновое уравнение

Гравитационные волновые уравнения являются уравнениями второго порядка в частных производных, которые описывают распространение гравитационных волн в свободном пространстве. В случае отсутствия зарядов и токов мы получаем однородные дифференциальные уравнения типа:

$- { 1 \over {c}^2 } {\partial^2 \over \partial t^2} \bigg) \mathbf{E_G} \ \ = \ \ 0$

$- { 1 \over {c}^2 } {\partial^2 \over \partial t^2} \bigg) \mathbf{B_G} \ \ = \ \ 0$,

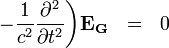
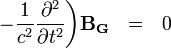где 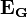$\mathbf{E_G}$ - градиентное гравитационное поле, а 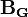$\mathbf{B_G}$ - роторное гравитационное поле.

Общее решение гравитационного волнового уравнения является суперпозицией следующих волн:

$\mathbf{E_G}( \mathbf{r}, t ) = g(\phi( \mathbf{r}, t )) = g( \omega t - \mathbf{k} \cdot \mathbf{r} )$

и

$\mathbf{B_G}( \mathbf{r}, t ) = g(\phi( \mathbf{r}, t )) = g( \omega t - \mathbf{k} \cdot \mathbf{r} )$

для произвольной хорошо ведущей себя функции g безразмерного аргумента φ / , где

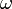$\ \omega$ - угловая частота (в радианах за секунду), и

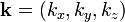$\mathbf{k} = ( k_x, k_y, k_z)$ - волновой вектор (в радианах на метр).

Учитывая следующие соотношения между индукциями и напряженностями полей в форме:

$\mathbf{B_G} = \mu_G\mathbf{H} \$

$\mathbf{D_G} = \epsilon_G\mathbf{E_G} \$,

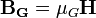
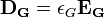можно получить следующие взаимные соответствия между градиентными и роторными гравитационными напряженностями:

$\sqrt{\mu_G}\mathbf{H_G} = \sqrt{\epsilon_G}\mathbf{E_G} \$.

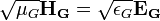Это уравнение определяет волновой импеданс в стандартном виде:

$\rho_G = \sqrt{\frac{\mu_G}{\epsilon_G}} = \frac{E_G}{H_G} \$.

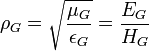LC контур

Гравитационное напряжение на гравитационной индуктивности:

$V_{GL} = -L_G\cdot \frac{d I_{GL}}{d t}. \$

Гравитационный ток через гравитационную емкость:

$I_{GL} = C_G\cdot \frac{d V_{GL}}{d t}. \$

Дифференцируя эти выражения по временной переменной, можно получить:

$\frac{d V_{GL}}{d t} = -L_G\frac{d^2I_{GL}}{dt^2} \$

$\frac{d I_{GL}}{d t} = C_G\frac{d^2V_{GL}}{dt^2}. \$

Учитывая следующие соотношения для амплитуд «напряжений» и «токов»:

$V_{GL} = V_{GC}; I_{GL} = I_{GC} \$

можно получить следующее дифференциальное уравнение для гравитационных осцилляций:

$\frac{d^2 I_G}{dt^2} + \frac{1}{L_GC_G}I_G = 0. \$

Более того, учитывая следующие взаимосвязи между «напряжениями» и «зарядами»:

$q_G = C_GV_G \$

а также «токами» и «магнитными потоками»:

$\phi_G = L_GI_G \$

уравнение осцилляций может быть переписано в зарядовой форме:

$\frac{d^2 q_G}{dt^2} + \frac{1}{L_GC_G}q_G = 0. \$

Это уравнение имеет частное решение:

$q_G(t) = A_0 Sin (\omega_{LC}t) \$

где

$\omega_{LC} = \frac{1}{\sqrt{L_GC_G}} \$

является резонансной частотой, а

$\rho_{LC} = \sqrt{\frac{L_G}{C_G}} \$

- гравитационным характеристическим импедансом.

Следует помнить, что в общем случае гравитационный заряд(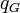$q_G \$) имеет ту же размерность величины, что и гравитационная масса ($m_G \$).

Смотри также

• Самосогласованные гравитационные константы
• Квантовый электромагнитный резонатор
• Электродинамика

Ссылки

1. ↑ K.T. McDonald, Am. J. Phys. 65, 7 (1997) 591-2.
2. ↑ O. Heaviside, Electromagnetic Theory (”The Electrician” Printing and Publishing Co., London, 1894) pp. 455-465.
3. ↑ W. K. H. Panofsky and M. Phillips, Classical Electricity and Magnetism (Addison-Wesley, Reading, MA, 1955), p. 168, 166.
4. ↑ R. L. Forward, Proc. IRE 49, 892 (1961).
5. ↑ R. M. Wald, General Relativity (University of Chicago Press, Chicago, 1984).
6. ↑ V. de Sabbata and M. Gasperini, Introduction to Gravitation (World Scientific, Singapore,1985).
7. ↑ V. de Sabbata and C.Sivaram, Spin and Torsion in Gravitation (World Scientific, Singapore,1994)
8. ↑ Raymond Y. Chiao. "Conceptual tensions between quantum mechanics and general relativity: Are there experimental consequences, e.g., superconducting transducers between electromagnetic and gravitational radiation?" arXiv:gr-qc/0208024v3 (2002).
9. ↑ R.Y. Chiao and W.J. Fitelson. Time and matter in the interaction between gravity and quantum fluids: are there macroscopic quantum transducers between gravitational and electromagnetic waves? In Proceedings of the “Time & Matter Conference” (2002 August 11-17; Venice, Italy), ed. I. Bigi and M. Faessler (Singapore: World Scientific, 2006), p. 85. arXiv: gr-qc/0303089.
10. ↑ R.Y. Chiao. Conceptual tensions between quantum mechanics and general relativity: are there experimental consequences? In Science and Ultimate Reality, ed. J.D. Barrow, P.C.W. Davies, and C.L.Harper, Jr. (Cambridge: Cambridge University Press, 2004), p. 254. arXiv:gr-qc/0303100.
11. ↑ Raymond Y. Chiao. "New directions for gravitational wave physics via “Millikan oil drops” arXiv:gr-qc/0610146v16 (2007).PDF</