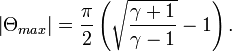Центрированная простая волна разрежения

Центрированная простая волна разрежения около острой кромки расширяющейся области

Течение Прандтля-Майера, или центрированная простая волна разрежения — течение, реализующееся в сверхзвуковом потоке около острой кромки расширяющейся области. Представляет собой бесконечный набор ударных волн, в каждой из которых поток изоэнтропически поворачивается на небольшой угол. Величина первого угла 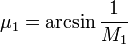$\mu_1=\arcsin{\frac{1}{M_1}}$, последнего — 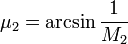$\mu_2=\arcsin{\frac{1}{M_2}}$. Предельный угол, на который может отклониться поток, зависит от показателя адиабаты γ и выражается формулой:

$\left|\Theta_{max}\right|=\frac{\pi}{2}\left(\sqrt\frac{\gamma+1}{\gamma-1}-1\right).$

Для воздуха (γ≈1,4) эта величина примерно равна 135°.

Особенность течения Прандтля-Майера в том, что оно является изоэнтропическим и все термодинамические параметры в нем являются функциями одного из них (простая волна).

Литература

Крайко А.Н. Краткий курс теоретической газовой динамики. — М.: МФТИ, 2007. — С. 300. — ISBN 978-5-7417-0229-1