- Теория Демпстера — Шафера
-
Теория Демпстера — Шафера
Демпстера-Шафера теория - это математическая теория очевидностей (свидетельств) ([SH76]), основанная на функции доверия (belief functions) и функции правдоподобия (plausible reasoning), которые используются, чтобы скомбинировать отдельные части информации (свидетельства) для вычисления вероятности события. Теория была развита Артуром П. Демпстером (Arthur P. Dempster) и Гленном Шафером (Glenn Shafer).
Содержание
Рассмотрим двух возможных игроков
Первая игра — подбрасывание монеты, где ставки делаются на то, выпадет орел или решка. Теперь представим вторую игру, в которой ставки принимаются на исход боя между лучшим в мире боксером и лучшим в мире борцом. Предположим, мы несведущи в боевых искусствах, и нам весьма трудно определиться на кого ставить.
Многие люди будут менее уверены в ситуации второй игры, в которой вероятности неизвестны, чем в первой игре, где легко увидеть, что вероятность каждого исхода равна половине. В случае второй игры, Байесовская теория присвоит каждому исходу половинную вероятность, вне зависимости от информации, делающей один из исходов более вероятным, чем другой. Теория Демпстера-Шафера позволяет определить степень уверенности, которую имеет игрок, относительно вероятностей присвоенных различным исходам.
Формализм
Пусть
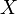 — универсальное множество, набор всех рассматриваемых утверждений. Показательное множество,
— универсальное множество, набор всех рассматриваемых утверждений. Показательное множество, 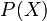 , совокупность всех подмножеств множества
, совокупность всех подмножеств множества 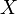 , включая пустое множество,
, включая пустое множество, 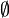 . Например, если:
. Например, если: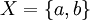
то
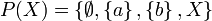
По определению, масса пустого множества — ноль:
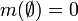
Массы оставшихся элементов показательного множества нормированы на единичную сумму:
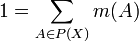
Масса
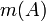 элемента показательного множества,
элемента показательного множества, 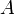 , выражает соотношение всех уместных и доступных свидетельств, которые поддерживают утверждение, что определенный элемент
, выражает соотношение всех уместных и доступных свидетельств, которые поддерживают утверждение, что определенный элемент 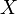 принадлежит
принадлежит 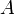 но не принадлежит ни одному подмножетсву
но не принадлежит ни одному подмножетсву 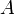 . Величина
. Величина 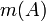 относится только к множеству
относится только к множеству 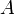 и не создает никаких дополнительных утверждений о других подмножествах
и не создает никаких дополнительных утверждений о других подмножествах 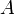 , каждое из которых, по определению, имеет свою собственную массу.
, каждое из которых, по определению, имеет свою собственную массу.Исходя из приписаных масс, могут быть определены верхняя и нижняя границы интервала возможностей. Этот интервал содержит точную величину вероятности рассматриваемого подмножетсва (в классическом смысле), и ограничена двумя неаддитивными непрерывными мерами, называеыми доверие (belief) (or поддержка (support)) and правдоподобие (plausibility):
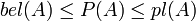
Доверие
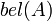 к множеству
к множеству 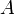 определяется как сумма всех масс собственных подмножеств рассматривеаемого множества:
определяется как сумма всех масс собственных подмножеств рассматривеаемого множества: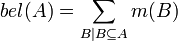
Правдоподобие
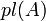 — это сумма масс всех множеств
— это сумма масс всех множеств 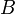 пересекающихся с рассматриваемым множеством
пересекающихся с рассматриваемым множеством 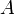 :
: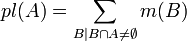
Эти две меры соотносятся между собой следующим образом:
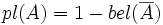
Из вышенаписанного следует, что достаточно знать хотя бы одну из мер (массу, доверие или правдоподобие), чтобы вычислить оставшиеся две.
Рассмотрим проблему объединения двух независимых множеств приписанных масс. Исходное правило объединения известное как Dempster's rule of combination является обобщением Bayes' rule. Это правило придает особое значение согласию между многочисленными источниками и игнорирует все конфликтующие свидетельства с помощью нормализации. Правомерность использования этого правила подвергается серьёзным сомнениям в случае значительных несоответствий между источниками информации.
Собственно, объединение (называемое присоединенная маса) вычисляется из двух множеств масс
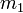 и
и 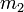 следующим образом:
следующим образом: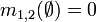
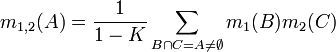
где:
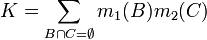
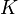 является мерой конфликта между двумя наборами масс. Нормализирующий множитель,
является мерой конфликта между двумя наборами масс. Нормализирующий множитель, 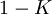 , соответствует полному игнорированию несоответствий и приписыванию любой массе, соответствующей конфликту, пустого множества. Следовательно, эта операция приводит к контринтуитивным результатам в случае значительного конфликта при определенных обстоятельствах.
, соответствует полному игнорированию несоответствий и приписыванию любой массе, соответствующей конфликту, пустого множества. Следовательно, эта операция приводит к контринтуитивным результатам в случае значительного конфликта при определенных обстоятельствах.Дискуссия
Поддержка и правдоподобность
Для примера, предположим мы имеем поддержку 0.5 и правдоподобие 0.8 для утверждения "кот в коробке мертв." Это означает, что у нас есть свидетельства, которые позволяют нам говорить, что утверждение истинно с уверенностью 0.5. Однако свидетельства в пользу противоположной гипотезы (т.е. "кот жив") имеют уверенность 0.2. Оставшаяся масса 0.3 (разрыв между поддержкой свидетельства 0.5 и противоположного свидетельства 0.2) является "неопределенностью" что означает что кот может быть либо быть живым либо быть мертвым. Этот интервал представляет собой уровень неопределенности, основанный на свидетельствах в данной системе.
Гипотеза Вероятность Поддержка Правдоподобие Ноль (ни жив ни мертв) 0 0 0 Жив 0.2 0.2 0.5 Мертв 0.5 0.5 0.8 Одновременно (жив и мертв) 0.3 1.0 1.0 Литература
- [DE68] Dempster, Arthur P.; A generalization of Bayesian inference, Journal of the Royal Statistical Society, Series B, Vol. 30, pp. 205-247, 1968
- [SH76] Shafer, Glenn; A Mathematical Theory of Evidence, Princeton University Press, 1976
- [SH02] Shafer, Glenn; Dempster-Shafer theory, 2002
См. также
- Possibility theory
- Probability theory
- Bayes' theorem
- Bayesian network
- Dezert-Smarandache theory, a generalised form of Dempster-Shafer theory
- G.L.S. Shackle
- Теория возможностей
- Эвентология
- Нечёткая логика
Wikimedia Foundation. 2010.
