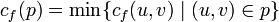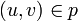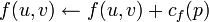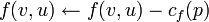Форда-Фалкерсона алгоритм
- Форда-Фалкерсона алгоритм
-
Алгоритм Форда — Фалкерсона решает задачу нахождения максимального потока в транспортной сети.
Идея алгоритма заключается в следующем. Изначально величине потока присваивается значение 0: f(u,v) = 0 для всех 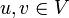 . Затем величина потока итеративно увеличивается посредством поиска увеличивающего пути (путь от источника s к стоку t, вдоль которого можно послать больший поток). Процесс повторяется, пока можно найти увеличивающий путь.
. Затем величина потока итеративно увеличивается посредством поиска увеличивающего пути (путь от источника s к стоку t, вдоль которого можно послать больший поток). Процесс повторяется, пока можно найти увеличивающий путь.
Алгоритм
Дан граф G(V,E) с пропускной способностью c(u,v) и потоком f(u,v) = 0 для ребер из u в v. Необходимо найти максимальный поток из источника s в сток t. На каждом шаге алгоритма действуют те же условия, что и для всех потоков:
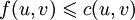 . Поток из u в v не превосходит пропускной способности.
. Поток из u в v не превосходит пропускной способности.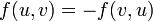 .
.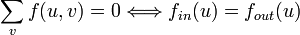 для всех узлов u, кроме s и t. Поток не изменяется при прохождении через узел.
для всех узлов u, кроме s и t. Поток не изменяется при прохождении через узел.
Остаточная сеть Gf(V,Ef) — сеть с пропускной способностью cf(u,v) = c(u,v) − f(u,v) и без потока.
Вход Граф 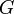 с пропускной способностью
с пропускной способностью  , источник
, источник  и сток
и сток 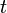
Выход Максимальный поток 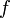 из
из  в
в 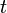
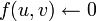 для всех ребер
для всех ребер 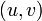
- Пока есть путь
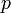 из
из  в
в 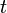 в
в 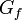 , такой что
, такой что 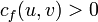 для всех ребер
для всех ребер 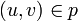 :
:
- Найти
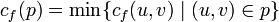
- Для каждого ребра
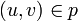
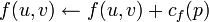
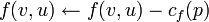
Путь может быть найден, например, поиском в ширину (алгоритм Эдмондса-Карпа) или поиском в глубину в Gf(V,Ef).
Сложность
Добавляя поток увеличивающего пути к уже имеющемуся потоку, максимальный поток будет получен, когда нельзя будет найти увеличивающий путь. Тем не менее, если величина пропускной способности — иррациональное число, то алгоритм может работать бесконечно. В целых числах таких проблем не возникает и время работы ограничено O(E*f), где E — число вершин в графе, f — максимальный поток в графе, так как каждый увеличивающий путь может быть найден за O(E) и увеличивает поток как минимум на 1.
Пример
Следующий пример показывает первые шаги алгоритма Форда-Фалкерсона в транспортной сети с четырьмя узлами, источником A и стоком D. Этот пример показывает худший случай. При использовании поиска в ширину алгоритму потребуется всего лишь 2 шага.
| Путь |
Пропускная способность |
Результат |
|
Начальная транспортная сеть |
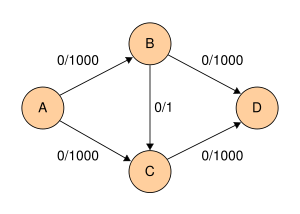 |
| A,B,C,D |
min(cf(A,B),cf(B,C),cf(C,D)) =
min(c(A,B) − f(A,B),c(B,C) − f(B,C),c(C,D) − f(C,D)) =
min(1000 − 0,1 − 0,1000 − 0) = 1 |
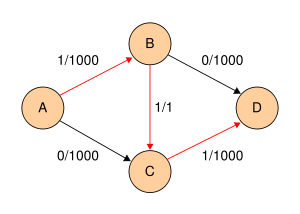 |
| A,C,B,D |
min(cf(A,C),cf(C,B),cf(B,D)) =
min(c(A,C) − f(A,C),c(C,B) − f(C,B),c(B,D) − f(B,D)) =
min(1000 − 0,0 − ( − 1),1000 − 0) = 1 |
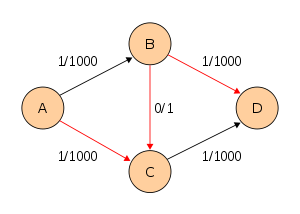 |
|
После 1998 шагов … |
|
|
Конечная сеть |
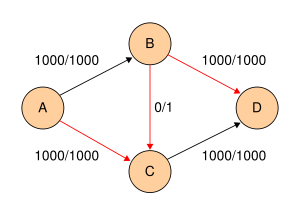 |
Cсылки
Литература
- Томас Х. Кормен и др. Алгоритмы: построение и анализ = INTRODUCTION TO ALGORITHMS. — 2-е изд. — М.: «Вильямс», 2006. — С. 1296. — ISBN 0-07-013151-1
Wikimedia Foundation.
2010.
Полезное
Смотреть что такое "Форда-Фалкерсона алгоритм" в других словарях:
Форда — Фалкерсона алгоритм — [Ford Fulkerson algorithm] способ решения задачи построения максимального потока в сети. (Поток в сети определяется пропускной способностью ее дуг от начальной вершины до конечной вершины.). Алгоритм Л.Форда и Д.Фалкерсона применяется, например … Экономико-математический словарь
Форда — Фалкерсона алгоритм — Способ решения задачи построения максимального потока в сети. (Поток в сети определяется пропускной способностью ее дуг от начальной вершины до конечной вершины.). Алгоритм Л.Форда и Д.Фалкерсона применяется, например, при решении транспортной… … Справочник технического переводчика
Алгоритм Форда — Фалкерсона — решает задачу нахождения максимального потока в транспортной сети. Идея алгоритма заключается в следующем. Изначально величине потока присваивается значение 0: f(u,v) = 0 для всех . Затем величина потока итеративно увеличивается посредством… … Википедия
Алгоритм Форда–Фалкерсона — решает задачу нахождения максимального потока в транспортной сети. Идея алгоритма заключается в следующем. Изначально величине потока присваивается значение 0: f(u,v) = 0 для всех . Затем величина потока итеративно увеличивается посредством… … Википедия
Форда-Фалкерсона теорема — Теорема Форда Фалкерсона теорема о максимальном потоке в графе. Звучит так: величина максимального потока равна величине минимального разреза. Достаточность: любой поток между вершинами t и s меньше или равен величине любого сечения. Пусть дан… … Википедия
Теорема Форда — Фалкерсона — теорема о максимальном потоке в графе. Звучит так: величина максимального потока не превышает величины минимального разреза. Достаточность: любой поток между вершинами t и s меньше или равен величине любого сечения. Пусть дан некоторый поток и… … Википедия
Теорема Форда–Фалкерсона — Теорема Форда Фалкерсона теорема о максимальном потоке в графе. Звучит так: величина максимального потока не превышает величины минимального разреза. Достаточность: любой поток между вершинами t и s меньше или равен величине любого сечения. Пусть … Википедия
Алгоритм Эдмондса — Карпа — Алгоритм Эдмондса Карпа решает задачу нахождения максимального потока в транспортной сети. Алгоритм представляет собой частный случай метода Форда Фалкерсона и работает за время O(VE2). Впервые был опубликован в 1970 году советским… … Википедия
Алгоритм Эдмондса — Алгоритм Эдмондса Карпа решает задачу нахождения максимального потока в транспортной сети. Алгоритм представляет собой частный случай метода Форда Фалкерсона и работает за время . Впервые был опубликован в 1970 году советским учёным Е … Википедия
Алгоритм проталкивания предпотока — решает задачу нахождения максимального потока в транспортной сети. Алгоритм не является частным случаем алгоритма Форда Фалкерсона. Реализованный без специальных усовершенствований, алгоритм выполняется за время . Некоторые усовершенствования ещё … Википедия
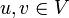 . Затем величина потока итеративно увеличивается посредством поиска увеличивающего пути (путь от источника s к стоку t, вдоль которого можно послать больший поток). Процесс повторяется, пока можно найти увеличивающий путь.
. Затем величина потока итеративно увеличивается посредством поиска увеличивающего пути (путь от источника s к стоку t, вдоль которого можно послать больший поток). Процесс повторяется, пока можно найти увеличивающий путь.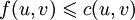 . Поток из u в v не превосходит пропускной способности.
. Поток из u в v не превосходит пропускной способности. .
.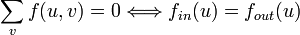 для всех узлов u, кроме s и t. Поток не изменяется при прохождении через узел.
для всех узлов u, кроме s и t. Поток не изменяется при прохождении через узел.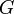 с пропускной способностью
с пропускной способностью  , источник
, источник  и сток
и сток 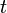
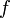 из
из  в
в 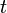
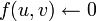 для всех ребер
для всех ребер 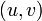
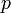 из
из  в
в 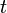 в
в 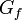 , такой что
, такой что 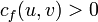 для всех ребер
для всех ребер 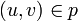 :
: