Алгоритм Эдмондса

Алгоритм Эдмондса — Карпа решает задачу нахождения максимального потока в транспортной сети. Алгоритм представляет собой частный случай метода Форда — Фалкерсона и работает за время $O(VE^2)$. Впервые был опубликован в 1970 году советским учёным Е. А. Диницом. Позже, в 1972 году, был независимо открыт Эдмондсом и Карпом.

Алгоритм

Алгоритм Эдмондса — Карпа — это вариант алгоритма Форда — Фалкерсона, при котором на каждом шаге выбирают кратчайший дополняющий путь из $s$ в $t$ в остаточной сети (полагая, что каждое ребро имеет единичную длину). Кратчайший путь находится поиском в ширину.

Описание

1. Обнуляем все потоки. Остаточная сеть изначально совпадает с исходной сетью.
2. В остаточной сети находим кратчайший путь из источника в сток. Если такого пути нет, останавливаемся.
3. Пускаем через найденный путь (он называется увеличивающим путём или увеличивающей цепью) максимально возможный поток:
   1. На найденном пути в остаточной сети ищем ребро с минимальной пропускной способностью $c_\min$.
   2. Для каждого ребра на найденном пути увеличиваем поток на $c_\min$, а в противоположном ему — уменьшаем на $c_\min$.
   3. Модифицируем остаточную сеть. Для всех рёбер на найденном пути, а также для противоположных им рёбер, вычисляем новую пропускную способность. Если она стала ненулевой, добавляем ребро к остаточной сети, а если обнулилась, стираем его.
4. Возвращаемся на шаг 2.

Чтобы найти кратчайший путь в графе, используем поиск в ширину:

1. Создаём очередь вершин О. Вначале О состоит из единственной вершины s.
2. Отмечаем вершину s как посещённую, без предка, а все остальные как непосещённые.
3. Пока очередь непуста, выполняем следующие шаги:
   1. Удаляем первую в очереди вершину u.
   2. Для всех рёбер (u, v), исходящих из вершины u, таких что вершина v ещё не посещена, выполняем следующие шаги:
      1. Отмечаем вершину v как посещённую, с предком u.
      2. Добавляем вершину v в конец очереди
      3. Если v=t, выходим из обоих циклов: мы нашли кратчайший путь.
4. Если очередь пуста, возвращаем ответ, что пути нет вообще и останавливаемся.
5. Если нет, идём от t к s, каждый раз переходя к предку. Возвращаем путь в обратном порядке.

Сложность

В процессе работы алгоритм Эдмондса — Карпа будет находить каждый дополняющий путь за время $O(E)$. Ниже мы докажем, что общее число увеличений потока, выполняемое данным алгоритмом, составляет $O(VE)$. Таким образом, сложность алгоритма Эдмондса — Карпа равна $O(VE^2)$.

Доказательство

Назовём расстоянием от вершины x до вершины у длину кратчайшего пути от x до y в остаточной сети. Если такого пути нет, будем считать расстояние бесконечным. Будем говорить, что y приблизилась к x (отдалилась от x), если расстояние от x до y уменьшилось (увеличилось). Будем говорить, что y ближе к x (дальше от x), чем z, если расстояние от x до y меньше (больше), чем расстояние от x до z.

Лемма. В ходе работы алгоритма ни одна вершина никогда не приближается к источнику. Доказательство. Пусть это не так, тогда при каком-то увеличении потока некоторые вершины приблизилась к источнику. Назовём их неправильными. Выберем ту из неправильных вершин, которая после увеличения потока оказалась ближе всех к источнику (если таких больше одной, то любую из них). Обозначим выбранную вершину через v. Рассмотрим кратчайший путь от s до v. Обозначим предпоследнюю вершину на этом пути через u, таким образом, путь имеет вид s-...-u-v. Поскольку u ближе к s, чем v, а v - ближайшая к s из неправильных вершин, u - вершина правильная. Обозначив расстояния от s до u и v до и после увеличения потока соответственно через $d_u\$, $d_u^'$, $d_v\$, $d_v^'$, имеем:

$d_v^' < d_v$

$d_u^' \ge d_u$

$d_v^' = d_u^' + 1$

, откуда

$d_v^ \ge d_u^ + 2$

Следовательно, до увеличения потока ребро (u, v) отсутствовало в остаточной сети. Чтобы оно появилось, увеличивающий путь должен был содержать ребро (v, u). Но в алгоритме Эдмондса — Карпа увеличивающий путь всегда кратчайший, следовательно,

$d_u = d_v + 1$

, что противоречит предыдущему неравенству. Значит, наше предположение было неверным. Лемма доказана.

Назовём критическим то из ребёр увеличивающего пути, у которого остаточная пропускная способность минимальна. Оценим, сколько раз некое ребро (u, v) может оказываться критическим. Пускай это произошло на итерации $t_1$, а в следующий раз на итерации $t_2$. Обозначая через $D_y(t)$ расстояние от s до y на итерации t, имеем:

$D_v(t_1) = D_u(t_1)+1$

$D_v(t_2) = D_u(t_2)+1$

Заметим, что на итерации $t_1$ критическое ребро исчезает из остаточной сети. Чтобы к моменту итерации $t_2$ ребро (u, v) в ней вновь появилось, необходимо, чтобы на какой-то промежуточной итерации $t_3$ был выбран увеличивающий путь, содержащий ребро (v, u). Следовательно,

$D_u(t_3) = D_v(t_3)+1$

Используя ранее доказанную лемму, получаем:

$D_v(t_2) = D_u(t_2)+1 \ge D_u(t_3)+1 = D_v(t_3)+2 \ge D_v(t_1)+2$

Поскольку изначально $D_v>0$ (иначе v=s, но ребро, ведущее в s, не может появиться на кратчайшем пути из s в t), и всегда, когда $D_v$ конечно, оно меньше V (кратчайший путь не содержит циклов, и, следовательно, содержит менее V ребёр), ребро может оказаться критическим не более $\frac{(V-1)-1}{2} + 1 = V/2$ раз. Поскольку каждый увеличивающий путь содержит хотя бы одно критическое ребро, а всего рёбер, которые могут когда-то стать критическими, $2E$ (все рёбра исходной сети и им противоположные), то мы можем увеличить путь не более ЕV раз. Следовательно, количество итераций не превышает O(EV), что и требовалось доказать.

Пример

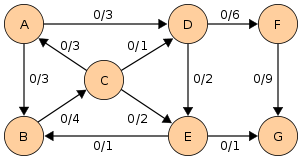
Пусть задана сеть с истоком в вершине $A$ и стоком в вершине $G$. На рисунке парой $f/c$ обозначен поток по этому ребру и его пропускная способность.

Поиск в ширину

Опишем поиск в ширину на первом шаге.

1. Очередь состоит из единственной вершины A. Посещена вершина A. Предков нет.
2. Очередь состоит (от начала к концу) из вершин B и D. Посещены вершины A,B,D. Вершины B,D имеют предка А.
3. Очередь состоит из вершин D и C. Посещены A,B,C,D. Вершины B,D имеют предка А, вершина C — предка B.
4. Очередь состоит из вершин C,E,F. Посещены A,B,C,D,E,F. Вершины B,D имеют предка А, вершина C — предка B, вершины E,F — предка D.
5. Вершина C удаляется из очереди: рёбра из неё ведут только в уже посещённые вершины.
6. Обнаруживается ребро (E,G) и цикл останавливается. В очереди вершины (F,G). Посещены все вершины. Вершины B,D имеют предка А, вершина C — предка B, вершины E,F — предка D, вершина G — предка E.
7. Идём по предкам: G->E->D->A. Возвращаем пройденный путь в обратном порядке: А->D->E->G.

Заметим, что в очередь последовательно добавляли вершины, достижимые из A ровно за 1 шаг, ровно за 2 шага, ровно за 3 шага. Кроме того, предком каждой вершины является вершина, достижимая из A ровно на 1 шаг быстрее.

Основной алгоритм

Пропускная способность пути	Путь
$\min(c_f(A,D),c_f(D,E),c_f(E,G)) =$ $\min(3-0, 2-0, 1-0) =$ $\min(3,2,1) = 1$	$A,D,E,G$
$\min(c_f(A,D),c_f(D,F),c_f(F,G)) =$ $\min(3-1, 6-0, 9-0) =$ $\min(2,6,9) = 2$	$A,D,F,G$
$\min(c_f(A,B),c_f(B,C),c_f(C,D),c_f(D,F),c_f(F,G)) =$ $\min(3-0, 4-0, 1-0, 6-2, 9-2) =$ $\min(3,4,1,4,7) = 1$	$A,B,C,D,F,G$
$\min(c_f(A,B),c_f(B,C),c_f(C,E),c_f(E,D),c_f(D,F),c_f(F,G)) =$ $\min(3-1, 4-1, 2-0, 0--1, 6-3, 9-3) =$ $\min(2,3,2,1,3,6) = 1$	$A,B,C,E,D,F,G$

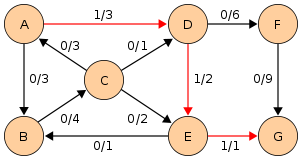
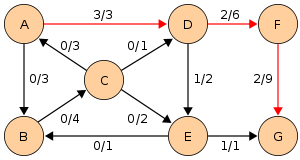
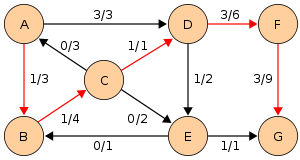
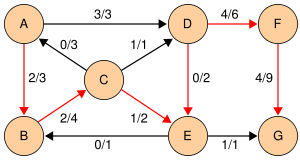
Отметим, что в процессе выполнения алгоритма длины дополняющих путей (на рисунках обозначены красным) не убывают. Это свойство выполняется благодаря тому, что мы ищем кратчайший дополняющий путь.

Алгоритм Диница

Основная статья: Алгоритм Диница

Улучшенной версией алгоритма Эдмондса-Карпа является алгоритм Диница, требующий $O(|V|^2|E|)$ операций.

Назовём вспомогательной бесконтурной сетью графа G с источником s его подграф, содержащий только такие рёбра (u, v), для которых минимальное расстояние от s до v на единицу больше минимального расстояния от s до u.

Алгоритм Диница:

1. Строим минимальную бесконтурную сеть остаточного графа.
2. Пока в сети есть путь из s в t, выполнить следующие шаги:
   1. Находим кратчайший путь из s в t. Если его нет, выйти из цикла.
   2. На найденном пути в остаточной сети ищем ребро с минимальной пропускной способностью $c_\min$.
   3. Для каждого ребра на найденном пути увеличиваем поток на $c_\min$, а в противоположном ему — уменьшаем на $c_\min$.
   4. Удаляем все рёбра, достигшие насыщения.
   5. Удаляем все тупики (то есть вершины, кроме стока, откуда не выходит рёбер, и вершины, кроме источника, куда рёбер не входит) вместе со всеми инцидентными им рёбрами.
   6. Повторяем предыдущий шаг, пока есть что удалять.
3. Если найденный поток ненулевой, добавляем его к общему потоку и возвращаемся на шаг 1.

Ссылки

• Реализация алгоритма Эдмондса-Карпа на C++ на сайте e-maxx.ru
• Визуализация алгоритма
• Реализация поиска максимального потока методом Эдмондса-Карпа на Java

Литература

• Томас Кормен и др. Алгоритмы: построение и анализ = INTRODUCTION TO ALGORITHMS. — 2-е изд. — М.: «Вильямс», 2006. — С. 1296. — ISBN 0-07-013151-1