- Условия Каруша — Куна — Таккера
-
Условия Каруша — Куна — Таккера
В теории оптимизации условия Каруша — Куна — Таккера (англ. Karush — Kuhn — Tucker conditions, KKT) — необходимые условия решения задачи нелинейного программирования. Чтобы решение было оптимальным, должны быть выполнены некоторые условия регулярности. Метод является обобщением метода множителей Лагранжа. В отличие от него, ограничения, накладываемые на переменные, представляют собой не уравнения, а неравенства.
Содержание
Постановка задачи
Рассмотрим задачу нелинейной оптимизации. Пусть есть функции
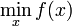 при условиях
при условиях 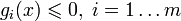 .
.
Вильям Каруш в своей дипломной работе нашёл необходимые условия в общем случае, когда накладываемые условия могут содержать и уравнения, и неравенства. Независимо от него к тем же выводам пришли Гарольд Кун и Альберт Таккер.
Необходимые условия минимума функции
Если
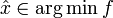 при наложенных ограничениях — решение задачи, то найдётся ненулевой вектор множителей Лагранжа
при наложенных ограничениях — решение задачи, то найдётся ненулевой вектор множителей Лагранжа 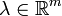 такой, что для функции Лагранжа
такой, что для функции Лагранжа 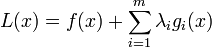 выполняются условия:
выполняются условия:- стационарности —
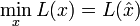 ;
; - дополняющей нежёсткости —
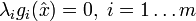 ;
; - неотрицательности —
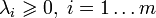 .
.
Достаточные условия минимума функции
Перечисленные необходимые условия минимума функции в общем случае не являются достаточными. Существует несколько вариантов дополнительных условий, которые делают их достаточными.
Простая формулировка
Если для допустимой точки
 выполняются условия стационарности, дополняющей нежёсткости и неотрицательности, а также λ1 > 0, то
выполняются условия стационарности, дополняющей нежёсткости и неотрицательности, а также λ1 > 0, то 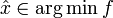 .
.Более слабые условия
Если для допустимой точки
 выполняются условия стационарности, дополняющей нежёсткости и неотрицательности, а также
выполняются условия стационарности, дополняющей нежёсткости и неотрицательности, а также 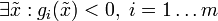 (условие Слейтера), то
(условие Слейтера), то 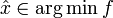 .
.
Wikimedia Foundation. 2010.
