- Приливы
-
Прили́в — периодическое колебание уровня океана или моря, обусловленное силами притяжения Луны и Солнца, а также другими приливообразующими силами. Приливы вызывают изменения в высоте уровня моря, а также периодические течения, известные как прили́вные течения, делающие предсказание приливов важным для прибрежной навигации.
Прили́вные изменения в каком-либо месте земного шара — результат изменения положений Луны и Солнца относительно Земли вкупе с эффектами вращения Земли и особенностями данного рельефа.
Хотя для земного шара сила тяготения Солнца почти в 200 раз больше, чем сила тяготения Луны, прили́вные силы, порождаемые Луной, почти вдвое больше порождаемых Солнцем. Это происходит из-за того, что приливные силы зависят не от величины гравитационного поля, а от степени его неоднородности (градиента). При увеличении расстояния до источника поля градиент уменьшается быстрее, чем величина самого поля. Поскольку Солнце почти в 400 раз дальше от Земли, чем Луна, то и приливные силы, вызываемые солнечным притяжением, слабее.
Содержание
История
Хосе де Акоста в своей Истории (1590), после открытия Ньютоном отливов и приливов, впервые объяснил их природу, периодичность и взаимосвязь с фазами Луны.
Терминология
 Малая вода (Бретань, Франция)
Малая вода (Бретань, Франция)Максимальный уровень поверхности воды во время прилива называется полной водой, а минимальный во время отлива — малой водой. В океане, где дно ровное, а суша далеко, полная вода проявляется как два «вздутия» водной поверхности: одно из них находится со стороны Луны, а другое — в противоположном конце земного шара. Также могут присутствовать ещё два меньших по размеру вздутия со стороны, направленной к Солнцу, и противоположной ему. Объяснение этому эффекту можно найти ниже, в разделе физика прилива.
Так как Луна и Солнце перемещаются относительно Земли, вместе с ними перемещаются и водные горбы, образуя прили́вные волны и прили́вные течения. В открытом море приливные течения имеют вращательный характер, а вблизи берегов и в узких заливах и проливах — возвратно-поступательный.
Если бы вся Земля была покрыта водой, мы бы наблюдали два регулярных прилива и отлива ежедневно. Но так как беспрепятственному распространению приливных волн мешают участки суши: острова и континенты, а также из-за действия силы Кориолиса на движущуюся воду, вместо двух приливных волн наблюдается множество маленьких волн, которые медленно (в большинстве случаев с периодом 12 ч 25,2 мин) обегают вокруг точки, называющейся амфидромической, в которой амплитуда прилива равна нулю. Доминирующая компонента прилива (лунный прилив М2) образует на поверхности Мирового океана около десятка амфидромических точек с движением волны по часовой стрелке и примерно столько же — против часовой (см. карту). Всё это делает невозможным предсказание времени прилива только на основе положений Луны и Солнца относительно Земли. Вместо этого используют «ежегодник приливов» — справочное пособие для вычисления времени наступления приливов и их высоты в различных пунктах земного шара. Также используются таблицы приливов, с данными о моментах и высотах малых и полных вод, вычисленными на год вперёд для основных прили́вных по́ртов.
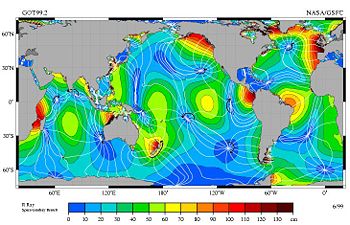 Cоставляющая прилива M2
Cоставляющая прилива M2Если соединить на карте точки с одинаковыми фазами прилива, мы получим так называемые котидальные линии, радиально расходящиеся из амфидромической точки. Обычно котидальные линии характеризуют положение гребня приливной волны для каждого часа. Фактически котидальные линии отражают скорость распространения приливной волны за 1 час. Карты, на которых представлены линии равных амплитуд и фаз приливных волн, называются котидальными картами.
Высота прилива — разница между высшим уровнем воды при приливе (полная вода) и низшим её уровнем при отливе (малая вода). Высота прилива — величина непостоянная, однако средний её показатель приводится при характеристике каждого участка побережья.
В зависимости от взаимного расположения Луны и Солнца малая и большая приливные волны могут усиливать друг друга. Для таких приливов исторически сложились специальные названия:
- Квадратурный прилив — наименьший прилив, когда приливообразующие силы Луны и Солнца действуют под прямым углом друг к другу (такое положение светил называется квадратурой).
- Сизигийный прилив — наибольший прилив, когда приливообразующие силы Луны и Солнца действуют вдоль одного направления (такое положение светил называется сизигией).
Чем меньше или больше прилив, тем меньше или, соответственно, больше отлив.
Самые высокие приливы в Мире
Можно наблюдать в бухте Фанди, которая находится на восточном побережье Канады между Нью-Брансуиком и Новой Шотландией.
Физика прилива
Приливообразующий потенциал
Пренебрегая размером, строением и формой Луны, запишем удельную силу притяжения пробного тела, находящегося на Земле. Пусть
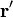 – радиус-вектор, направленный от пробного тела в сторону Луны, r' – длина этого вектора. В этом случае сила притяжения этого тела Луной будет равна
– радиус-вектор, направленный от пробного тела в сторону Луны, r' – длина этого вектора. В этом случае сила притяжения этого тела Луной будет равна
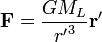 (1)
(1)где GML – селенометрическая гравитационная постоянная. Пробное тело поместим в точку P. Сила притяжения пробного тела, помещенного в центр масс Земли будет равна
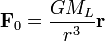 (2)
(2)Здесь под
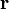 и r понимаются радиус-ветор, соединяющий центры масс Земли и Луны, и их абсолютные величины. Приливной силой мы будем называть разность этих двух сил тяготения
и r понимаются радиус-ветор, соединяющий центры масс Земли и Луны, и их абсолютные величины. Приливной силой мы будем называть разность этих двух сил тяготения
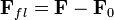 (3)
(3)В формулах (1) и (2) Луна считается шаром со сферически-симметричным распределением масс. Силовая функция притяжения пробного тела Луной ничем не отличается от силовой функции притяжения шара и равна
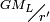 Вторая сила приложена к центру масс Земли и является строго постоянной велиной. Для получения силовой функции для этой силы мы введем временную систему координат. Ось Ox проведем из центра Земли и направим в сторону Луны. Направления двух других осей оставим произвольными. Тогда силовая функция силы
Вторая сила приложена к центру масс Земли и является строго постоянной велиной. Для получения силовой функции для этой силы мы введем временную систему координат. Ось Ox проведем из центра Земли и направим в сторону Луны. Направления двух других осей оставим произвольными. Тогда силовая функция силы 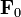 будет равна
будет равна 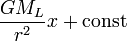 . Приливообразующий потенциал будет равен разности этих двух силовых функций. Обозначим его δW, будем иметь
. Приливообразующий потенциал будет равен разности этих двух силовых функций. Обозначим его δW, будем иметь 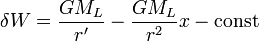 Постоянную
Постоянную 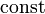 определим из условия нормировки, согласно которому приливнообразующий потенциал в центре Земли равен нулю. В центре Земли x = 0, r' = r Отсюда следует, что
определим из условия нормировки, согласно которому приливнообразующий потенциал в центре Земли равен нулю. В центре Земли x = 0, r' = r Отсюда следует, что 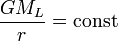 . Следовательно, мы получаем окончательную формулу приливообразующего потенциала в виде
. Следовательно, мы получаем окончательную формулу приливообразующего потенциала в виде 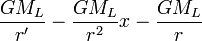 (4)
(4)Поскольку
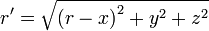
то
![\frac{1}{r'}=\frac{1}{r}{{\left[ {{\left( 1-\frac{x}{r} \right)}^{2}}+\frac{{{y}^{2}}+{{z}^{2}}}{{{r}^{2}}} \right]}^{-\frac{1}{2}}}](/pictures/wiki/files/49/1606089b1a99f089355b71ac4e184d5f.png)
При малых величинах
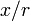 ,
, 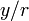 ,
, 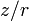 последнее выражение можно представить в следующем виде
последнее выражение можно представить в следующем виде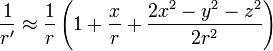 (5)
(5)Подставив (5) в (4), получим
 (6)
(6)Деформация поверхности планеты под действием прилива
Возмущающее воздействие приливного потенциала деформирует уровненную поверхность планеты. Оценим это воздействие, считая, что Земля представляет собой шар со сферически-симметричным распределением массы. Невозмущенный гравитационный потенциал Земли на поверхности будет равен
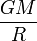 . Для точки P. , находящейся на расстоянии ρ от центра сферы, гравитационный потенциал Земли равен
. Для точки P. , находящейся на расстоянии ρ от центра сферы, гравитационный потенциал Земли равен 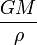 . Сократив на гравитационную постоянную, получим
. Сократив на гравитационную постоянную, получим  . Здесь переменными величинами являются x,y,z и ρ. Обозначим отношение масс гравитирующего тела к массе планеты греческой буквой μ и решим полученное выражение относительно ρ:
. Здесь переменными величинами являются x,y,z и ρ. Обозначим отношение масс гравитирующего тела к массе планеты греческой буквой μ и решим полученное выражение относительно ρ: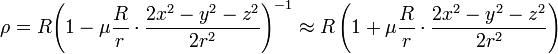
Так как ρ2 = x2 + y2 + z2 с той же степенью точности получим
Учитывая малость отношения
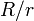 последние выражения можно записать так
последние выражения можно записать так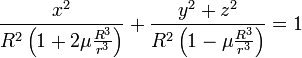
Мы получили, таким образом, уравнение двухосного эллипсоида, у которого ось вращения совпадает с осью Ox, т.е с прямой, соединяющей тяготеющее тело с центром Земли. Полуоси этого эллипсоида, очевидно, равны
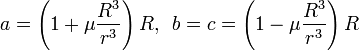
Приведем в конце небольшую численную иллюстрацию данного эффекта. Вычислим приливной «горб» на Земле, вызванный притяжением Луны. Радиус Земли равен R = 6378 км, расстояние между центрами Земли и Луны с учетом нестабильности лунной орбиты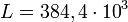 км, отношение массы Земли к массе Луны равно 81:1. Очевидно, что при подстановке в формулу мы получим величину, примерно равную 36 см.
км, отношение массы Земли к массе Луны равно 81:1. Очевидно, что при подстановке в формулу мы получим величину, примерно равную 36 см.См. также
Cсылки
Луна Физические
особенностиВнутренняя структура • Гравитация • Топография • Магнитное поле • Атмосфера 
Орбита Орбита • Фазы • Новолуние • Полнолуние • Солнечное затмение • Лунное затмение • Прилив Лунная
поверхностьСеленография • Видимая сторона • Обратная сторона • Моря • Ударный кратер • Бассейн Южный полюс — Эйткен • Шеклтон • Лёд • Пик вечного света • Космическая погода • Кратковременные лунные явления Наука о Луне Геология (хронология) • Минералогия • Теория гигантского столкновения • KREEP • ALSEP • Лазерная локация Луны • Поздняя тяжёлая бомбардировка • Лунные породы • Реголит • Метеориты Исследование Исследование • Проект Аполлон • Колонизация • Лунный заговор Другое Календарь • Месяц • Полумесяц • Мифология • Искусство • Иллюзия Луны • Происхождение См. также: Солнечная система • Спутники планет • {{Исследование Луны АМС}}
Wikimedia Foundation. 2010.
