Признак Эйзенштейна

Крите́рий Э́йзенштейна — признак неприводимости многочлена. Несмотря на (традиционное) название, является именно признаком, то есть достаточным условием — но вовсе не необходимым, как можно было бы предположить, исходя из математического оттенка слова "критерий" (см. ниже).

Формулировка

Пусть a(x) = a₀ + a₁x + ... + a_nxⁿ - многочлен над факториальным кольцом R (n > 0), и для некоторого неприводимого элемента p выполняются следующие условия:

• $p\not|a_n$,
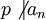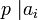• $~p~|a_i$ для любого i от 0 до n-1,
• $p^2\not|a_0$.

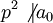Тогда многочлен a(x) неприводим над F — полем частных кольца R.

Наиболее часто этот критерий применяется, когда R — кольцо целых чисел 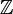$\Z$, а F — поле рациональных чисел $\mathbb Q$.

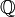Доказательство

Предположим обратное: a(x) = f(x)g(x), где f(x) = b₀ + b₁x + ... + b_kx^k и g(x) = c₀ + c₁x + ... + c_mx^m многочлены над F ненулевых степеней. Из леммы Гаусса следует, что их можно рассматривать как многочлены над R. Имеем:

a₀ = b₀c₀

По условию p | a₀ и R факториально, поэтому либо p | b₀ либо p | c₀, но не то и другое вместе ввиду того, что 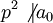$p^2\not|a_0$. Пусть p | b₀ и 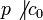$p\not|c_0$. Все коэффициенты f(x) не могут делиться на p, так как иначе бы это было бы верно для a(x). Пусть i — минимальный индекс, для которого b_i не делится на p. Отсюда следует:

a_i = b_ic₀ + b_{i − 1}c₁ + ...

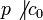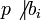Так как p | a_i и p | b_j для всех j < i то p | b_ic₀, но это невозможно, так как по условию $p\not|c_0$ и $p\not|b_i$. Теорема доказана.

Примеры

• Многочлен x³ + 2 неприводим над Q, из этого следует невозможность решения задачи об удвоении куба
• Многочлен деления круга f(x) = x^{p − 1} + x^{p − 2} + ...1 неприводим. В самом деле, если он приводим, то приводим и многочлен 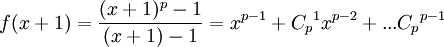$f(x+1)=\frac {(x+1)^p - 1}{(x+1) - 1}=x^{p-1}+{C_p}^1x^{p-2}+...{C_p}^{p-1}$, а так как все его коэффициенты, кроме первого являются биномиальными, то есть делятся на p 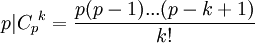$p|{C_p}^k=\frac{p(p-1)...(p-k+1)}{k!}$, а последний коэффициент 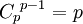${C_p}^{p-1}=p$ к тому же не делится на p², то по критерию Эйзенштейна он неприводим вопреки предположению.
• Многочлен x³ + 4 над Q является примером, показывающим, что критерий Эйзенштейна ("существует такое p, что ...; тогда многочлен неприводим") является только достаточным, но не необходимым условием. Действительно, единственный простой делитель свободного члена это p = 2, но 4 делится на 2² -- поэтому критерий Эйзенштейна здесь неприменим. С другой стороны, как многочлен 3 степени без рациональных корней, этот многочлен неприводим.