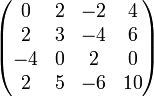- Полный ранг
-
Пусть задана любая матрица А с m строк и n столбцов. Рангом системы строк (столбцов) матрицы А называется максимальное число линейно независимых строк(столбцов). Несколько строк (столбцов) называются линейно-независимыми, если не одна из них не выражается линейно через другие. Ранг системы строк всегда равен рангу системы столбцов и это число называется рангом матрицы. Ранг матрицы — наивысший из порядков миноров этой матрицы, отличных от нуля. Ранг матрицы равен наибольшему числу линейно независимых строк (или столбцов) матрицы.
Обычно ранг матрицы A обозначается
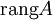 (
(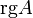 ) или
) или 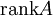 . Оба обозначения пришли к нам из иностранных языков, потому и употребляться могут оба. Последний вариант свойственен для английского языка, в то время как первый — для немецкого, французского и ряда других языков.
. Оба обозначения пришли к нам из иностранных языков, потому и употребляться могут оба. Последний вариант свойственен для английского языка, в то время как первый — для немецкого, французского и ряда других языков.Содержание
Определение
Пусть
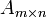 — прямоугольная матрица.
— прямоугольная матрица.Тогда по определению рангом матрицы A является:
- нуль, если A — нулевая матрица;
- число
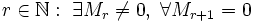 , где Mr — минор матрицы A порядка r, а Mr + 1 — окаймляющий к нему минор порядка (r + 1), если они существуют.
, где Mr — минор матрицы A порядка r, а Mr + 1 — окаймляющий к нему минор порядка (r + 1), если они существуют.
Теорема (о корректности определения рангов). Пусть все миноры матрицы
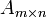 порядка k равны нулю (Mk = 0). Тогда
порядка k равны нулю (Mk = 0). Тогда 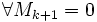 , если они существуют.
, если они существуют.Связанные определения
- Ранг
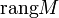 матрицы M размера
матрицы M размера 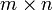 называют полным, если
называют полным, если 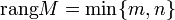 .
. - Базисный минор матрицы A — любой минор матрицы A порядка r, где
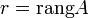 .
.
- Строки и столбцы, на пересечении которых стоит базисный минор, называются базисными строками и столбцами. (Они определены неоднозначно в силу неоднозначности базисного минора.)
Пример
Матрица
имеет ранг 2, так как есть минор второго порядка, отличный от нуля, а миноров третьего порядка нет.
Свойства
- Теорема (о базисном миноре): Пусть
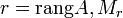 — базисный минор матрицы A, тогда:
— базисный минор матрицы A, тогда:
- базисные строки и базисные столбцы линейно независимы;
- любая строка (столбец) матрицы A есть линейная комбинация базисных строк (столбцов).
- Следствия:
- Если ранг матрицы равен r, то любые p:p > r строк или столбцов этой матрицы будут линейно зависимы.
- Если A — квадратная матрица, и
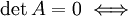 строки и столбцы этой матрицы линейно зависимы.
строки и столбцы этой матрицы линейно зависимы. - Пусть
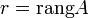 , тогда максимальное количество линейно независимых строк (столбцов) этой матрицы равно r.
, тогда максимальное количество линейно независимых строк (столбцов) этой матрицы равно r.
- Теорема (об инвариантности ранга при элементарных преобразованиях): Введём обозначение
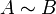 для матриц, полученных друг из друга элементарными преобразованиями. Тогда справедливо утверждение: Если
для матриц, полученных друг из друга элементарными преобразованиями. Тогда справедливо утверждение: Если 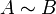 , то их ранги равны
, то их ранги равны - Теорема Кронекера — Капелли: Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы. В частности:
- Количество главных переменных системы равно рангу системы.
- Совместная система будет определена (её решение единственно), если ранг системы равен числу всех её переменных.
См. также
Ссылки
Wikimedia Foundation. 2010.