Полный порядок

В математике частично упорядоченным множеством называется множество, на котором определено отношение частичного порядка. Неформально можно сказать, что это отношение вводит некую иерархию элементов множества, выстраивает зависимости между ними, показывает, какой элемент множества «больше», а какой «меньше». При этом такое отношение вовсе не обязано быть отношением линейного порядка, т.е. не все элементы «сравнимы».

Формальное определение

Частичный порядок — это бинарное отношение R (обычно обозначаемое как 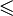$\leqslant$, «меньше или равно») на множестве P, обладающее свойствами рефлексивности, антисимметричности и транзитивности, то есть удовлетворяющее следующим аксиомам:

1. Рефлексивность: $\forall a \in P \quad a \leqslant a$;
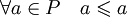2. Антисимметричность: $\forall a, b \in P \quad (a \leqslant b) \land (b \leqslant a) \Leftrightarrow a = b$;
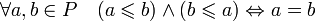3. Транзитивность: $\forall a, b, c \in P \quad (a \leqslant b) \land (b \leqslant c) \Rightarrow a \leqslant c$.

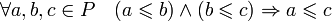Если 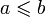$a \leqslant b$ и при этом 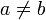$a \neq b$, то обычно пишут a < b («меньше», «строго меньше»). Вместо 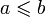$a \leqslant b$ также пишут 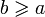$b \geqslant a$. Если же для любых двух элементов множества a и b верно либо a < b, либо a = b, либо a > b, такое отношение называется отношением линейного порядка. Иногда, когда из контекста ясно, что речь идёт именно о частично упорядоченных множествах, слово «частично» опускают.

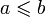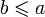Пары элементов, для которых не выполняется ни $a\leqslant b$, ни $b\leqslant a$, называются несравнимыми. В линейно упорядоченных множествах таких пар нет.

Примеры

Подмножества {x,y,z}, упорядоченные отношением включения

• Натуральные числа с отношением 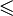$\leqslant$ (линейный порядок).

• Натуральные числа с отношением «делит» (только частичный порядок: например, несравнимы 4 и 5).

• Множество подмножеств данного множества с отношением включения ($\subseteq$).

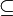Минимальный и наименьший элементы множества

В отличие от линейно упорядоченных множеств, для частично упорядоченных множеств различают понятия минимального и наименьшего элементов. Наименьшим элементом множества называется элемент, меньший всех остальных элементов. Минимальным элементом называется элемент, меньше которого во множестве нет. Наименьших элементов во множестве может быть не более одного, в то время как минимальных может быть много. Легко показать, что если во множестве есть наименьший элемент, он является и единственным минимальным. Если же минимальных элементов несколько, то все они несравнимы.

Аналогично вводятся понятия максимального и наибольшего элементов.

Пример 1. Для множества подмножеств {x, y, z} с отношением 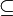$\subseteq$, изображённого на рисунке, единственным наименьшим и минимальным элементом является 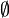$\emptyset$. Для множества непустых подмножеств наимешьшего нет, а минимальными будут {x}, {y}, {z}.

Пример 2. Для натуральных чисел с отношением делимости, единственным наименьшим и минимальным элементом является 1. Для натуральных чисел, больших 1, с тем же порядком, наименьшего элемента нет, а минимальными являются простые числа, т.к. они не делятся ни на какие другие элементы.

Строгий и нестрогий порядки

Иногда описанный здесь порядок называется нестрогим (или рефлексивным). В противовес ему существует понятие строгого (или иррефлексивного) частичного порядка — это отношение, удовлетворяющее только последним двум из приведённого списка аксиом.

Если R является нестрогим порядком, то 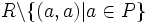$R \backslash \{(a,a)| a \in P\}$ — это соответствующий ему строгий порядок. Подобным образом и нестрогий порядок ставится в соответствие строгому.

Литература

• Н. К. Верещагин, А. Шень. Лекции по математической логике и теории алгоритмов. Часть 1. Начала теории множеств. М.: МЦНМО, 2002.