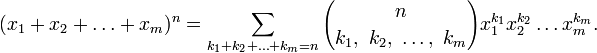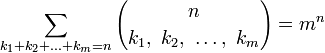Полиномиальный коэффициент

Мультиномиальные коэффициенты — коэффициенты в разложении 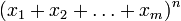$(x_1+x_2+\dots + x_m)^n$ по мономам $x_1^{k_1} x_2^{k_2}\dots x_m^{k_m}$:

$(x_1+x_2+\dots + x_m)^n = \sum_{k_1+k_2+\dots+k_m=n} {n\choose k_1,\ k_2,\ \dots,\ k_m} x_1^{k_1} x_2^{k_2}\dots x_m^{k_m}.$

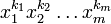Значение мультиномиального коэффициента 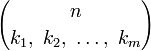${n\choose k_1,\ k_2,\ \dots,\ k_m}$ определено для всех целых неотрицательных чисел n и 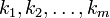$k_1, k_2, \dots, k_m$ таких, что $k_1+k_2+\dots+k_m=n$:

${n\choose k_1,\ k_2,\ \dots,\ k_m} = \frac{n!}{k_1!k_2!\dots k_m!}$.

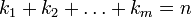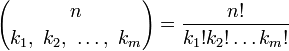Биномиальный коэффициент 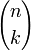${n\choose k}$ для неотрицательных n,k является частным случаем мультиномиального коэффициента (для m = 2), а именно

${n\choose k} = {n\choose k,\ n-k}$.

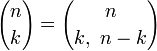В комбинаторном смысле мультиномиальный коэффициент 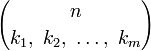${n\choose k_1,\ k_2,\ \dots,\ k_m}$ равен числу упорядоченных разбиений n-элементного множества на m подмножеств мощностей $k_1, k_2, \dots, k_m$.

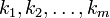Свойства

$\sum_{k_1+k_2+\dots+k_m=n} {n\choose k_1,\ k_2,\ \dots,\ k_m} = m^n$

См. также

• Мультиномиальное распределение.