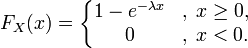Показательное распределение

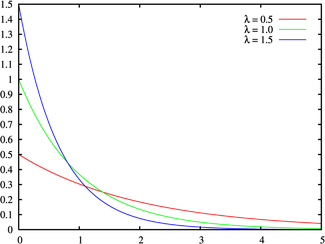
Показательное распределение

Плотность вероятности
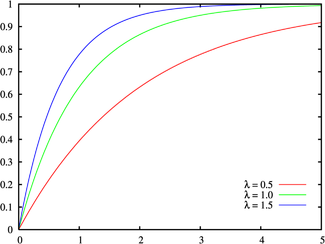
Функция распределения
Параметры	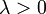$\lambda > 0 \,$ - интенсивность или обратный коэффициент масштаба
Носитель	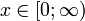$x \in [0;\infty)\!$
Плотность вероятности	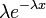$\lambda e^{-\lambda x}\,$
Функция распределения	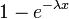$1 - e^{-\lambda x}\,$
Математическое ожидание	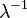$\lambda^{-1}\,$
Медиана	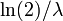$\ln(2)/\lambda\,$
Мода	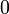$0\,$
Дисперсия	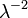$\lambda^{-2}\,$
Коэффициент асимметрии	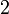$2\,$
Коэффициент эксцесса	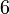$6\,$
Информационная энтропия	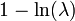$1 - \ln(\lambda)\,$
Производящая функция моментов	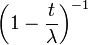$\left(1 - \frac{t}{\lambda}\right)^{-1}\,$
Характеристическая функция	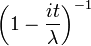$\left(1 - \frac{it}{\lambda}\right)^{-1}\,$

Показательное распределение — абсолютно непрерывное распределение, моделирующее время между двумя последовательными свершениями одного и того же события.

Определение

Случайная величина X имеет экспоненциальное распределение с параметром λ > 0, если её плотность имеет вид

$f_X(x) = \left\{\begin{matrix} \lambda \,e^{-\lambda x} &,\; x \ge 0, \\ 0 &,\; x < 0. \end{matrix}\right.$.

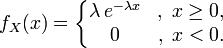Иногда семейство экспоненциальных распределений параметризуют обратным параметром 1 / λ:

$f_X(x) = \left\{\begin{matrix} {1 \over \lambda} \,e^{-{ x \over \lambda}} &,\; x \ge 0, \\ 0 &,\; x < 0. \end{matrix}\right.$.

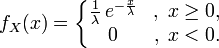Оба способа одинаково естественны, и необходима лишь договорённость, какой из них используется.

Пример. Пусть есть магазин, в который время от времени заходят покупатели. При определённых допущениях время между появлениями двух последовательных покупателей будет случайной величиной с экспоненциальным распределением. Среднее время ожидания нового покупателя (см. ниже) равно 1 / λ. Сам параметр λ тогда может быть интерпретирован, как среднее число новых покупателей за единицу времени.

В этой статье для определённости будем предполагать, что плотность экспоненциальной случайной величины X задана первым уравнением, и будем писать: $X \sim \mathrm{Exp}(\lambda)$.

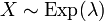Функция распределения

Интегрируя плотность, получаем функцию экспоненциального распределения:

$F_X(x) = \left\{\begin{matrix} 1-e^{-\lambda x}&,\; x \ge 0, \\ 0 &,\; x < 0. \end{matrix}\right.$

Моменты

Несложным интегрированием находим, что производящая функция моментов для экспоненциального распределения имеет вид:

$\mathrm{M}_X(t) = \left(1 - {t \over \lambda}\right)^{-1}$,

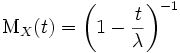откуда получаем все моменты:

$\mathbb{E}\left[X^n\right] = \frac{n!}{\lambda^n}$.

В частности,

$\mathbb{E}[X] = \frac{1}{\lambda}$,

$\mathrm{D}[X] = \frac{1}{\lambda^2}$.

Отсутствие памяти

Пусть 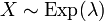$X \sim \mathrm{Exp}(\lambda)$. Тогда $\mathbb{P}(X > s+t \mid X > s) = \mathbb{P}(X > t)$.

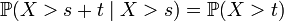Пример. Пусть автобусы приходят на остановку случайно, но с некоторой фиксированной средней интенсивностью. Тогда количество времени, уже затраченное пассажиром на ожидание автобуса, не влияет на время, которое ему ещё придётся прождать.

Связь с другими распределениями

• Минимум независимых экспоненциальных случайных величин также экспоненциальная случайная величина. Пусть 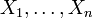$X_1, \ldots, X_n$ независимые случайные величины, и 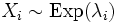$X_i \sim \mathrm{Exp}(\lambda_i)$. Тогда

$Y = \min\limits_{i=1,\ldots,n}(X_i) \sim \mathrm{Exp}\left(\sum\limits_{i=1}^n \lambda_i\right)$.

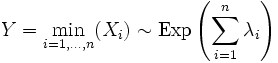• Экспоненциальное распределение является частным случаем Гамма распределения:

$\mathrm{Exp}(\lambda) \equiv \Gamma(1, \lambda)$.

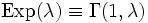• Сумма независимых одинаково распределённых экспоненциальных случайных величин имеет Гамма распределение. Пусть 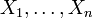$X_1, \ldots, X_n$ независимые случайные величины, и 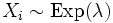$X_i \sim \mathrm{Exp}(\lambda)$. Тогда

$Y = \sum\limits_{i=1}^n X_i \sim \Gamma(n, \lambda)$.

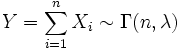• Экспоненциальное распределение может быть получено из непрерывного равномерного распределения методом обратного преобразования. Пусть $U \sim U[0,1]$. Тогда

$X = - \frac{1}{\lambda} \ln U \sim \mathrm{Exp}(\lambda)$.

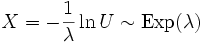• Экспоненциальное распределение с параметром λ = 1 / 2 — это частный случай распределения хи-квадрат:

$\mathrm{Exp}(1/2) \equiv \chi^2(2)$.

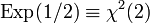Вероятностные распределения Одномерные Многомерные Дискретные: Бернулли | биномиальное | геометрическое | гипергеометрическое | логарифмическое | отрицательное биномиальное | Пуассона | равномерное мультиномиальное Абсолютно непрерывные: Бета | Вейбулла | Гамма | Колмогорова | Коши | Лапласа | логнормальное | Лоренца | нормальное (Гаусса) | равномерное | Парето | Стьюдента | Фишера | хи-квадрат | экспоненциальное | Эрланга многомерное нормальное

править