Особая точка дифференциального уравнения
- Особая точка дифференциального уравнения
-
В математике, осо́бой то́чкой векторного поля называется точка, в которой векторное поле равно нулю. Траектория соответствующего автономного обыкновенного дифференциального уравнения, стартующая из особой точки, остается неподвижной — то есть особая точка является неподвижной точкой фазового потока. В любой малой окрестности фазового пространства, не содержащей особых точек, векторное поле можно выпрямить подходящей заменой координат — тем самым, поведение системы вне особых точек устроено очень просто. Напротив, в окрестности особой точки система может обладать очень сложной динамикой. Говоря о свойствах особых точек векторных полей, обычно подразумевают свойства соответствующей системы в малой окрестности особой точки.
Особые точки линейных систем на плоскости
Простейшими примерами особых точек являются особые точки линейных векторных полей на плоскости.
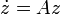 ,
,
где z = (x,y) — точка на двумерной плоскости, A — матрица 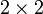 . Очевидно, точка z = (0,0) является единственной особой точкой такого уравнения.
. Очевидно, точка z = (0,0) является единственной особой точкой такого уравнения.
В зависимости от собственных значений матрицы A, особая точка линейного поля орбитально-топологически эквивалентна одному из четырёх типов: узел, седло, фокус, центр.
| Тип собственных значений |
Тип особой точки |
| Чисто мнимые |
Центр |
| Комплексные с отрицательной действительной частью |
Устойчивый фокус |
| Комплексные с положительной действительной частью |
Неустойчивый фокус |
| Действительные отрицательные |
Устойчивый узел |
| Действительные положительные |
Неустойчивый узел |
| Действительные разных знаков |
Седло |
Wikimedia Foundation.
2010.
Полезное
Смотреть что такое "Особая точка дифференциального уравнения" в других словарях:
Особая точка — в математике. 1) Особая точка кривой, заданной уравнением F (x, у) = 0, точка М0(х0, y0), в которой обе частные производные функции F (x, у) обращаются в нуль: Если при этом не все вторые частные производные… … Большая советская энциклопедия
ОСОБАЯ ТОЧКА — 1) О. т. аналитической функции f(z) препятствие для аналитического продолжения элемента функции f(z) комплексного переменного zвдоль какого либо пути на плоскости этого переменного. Пусть аналитическая функция f(z) определена некоторым… … Математическая энциклопедия
ПОДВИЖНАЯ ОСОБАЯ ТОЧКА — особая точка z0 решения дифференциального уравнения F(z, w, w )=0 (F аналитич. функция), рассматриваемого как функция w(z).комплексного переменного z, при условии, что решения того же уравнения с близкими начальными данными имеют близкие к z0… … Математическая энциклопедия
Фуксова особая точка — В теории дифференциальных уравнений с комплексным временем, точка называется фуксовой особой точкой линейного дифференциального уравнения если матрица системы A(t) имеет в ней полюс первого порядка. Это простейшая возможная особенность… … Википедия
НЕПОДВИЖНАЯ ОСОБАЯ ТОЧКА — общая особая точка всех решений дифференциального уравнения (F аналитич. ция), рассматриваемых как функции комплексного переменного z, начальные условия к рых пробегают нек рую область в пространстве (z, w). Лит.:[1] Голубев В. В., Лекции по… … Математическая энциклопедия
Неподвижная точка — Отображение с тремя неподвижными точками В математике, неподвижная точка отображения точка, которую отображение переводит в неё же, иными словами, решение уравнения … Википедия
РАНГ — линейного обыкновенного дифференциального уравнения в комплексной области (1) число r=k+1, где Коэффициенты уравнения (1) сходящиеся при больших ряды Понятие Р. употребляется только тогда, когда особая точка дифференциального уравнения (1). Р.… … Математическая энциклопедия
ВЫРОЖДЕННОЕ ГИПЕРГЕОМЕТРИЧЕСКОЕ УРАВНЕНИЕ — конфлюэнтное уравнение линейное обыкновенное дифференциальное уравнение 2 го порядка или, в самосопряженной форме, Переменные и параметры в общем случае могут принимать любые комплексные значения. Приведенной формой уравнения (1) является… … Математическая энциклопедия
Узел — I Узел в технике, 1) часть машины, механизма, установки и т. п., состоящая из нескольких более простых элементов (деталей) и представляющая собой сборочную единицу, входящую в Агрегат. 2) Совокупность связанных между собой и расположенных … Большая советская энциклопедия
Центр — I (лат. centrum, от греч. kéntron срединная точка, средоточие, центр) 1) середина, средняя часть чего либо (Ц. города, Ц. поля). 2) Населённый пункт (например, областной Ц.). 3) Место сосредоточения какой либо деятельности, органов… … Большая советская энциклопедия
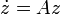 ,
,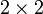 . Очевидно, точка z = (0,0) является единственной особой точкой такого уравнения.
. Очевидно, точка z = (0,0) является единственной особой точкой такого уравнения.